この記事ではインダクタの等価回路について説明します。
理想のインダクタ
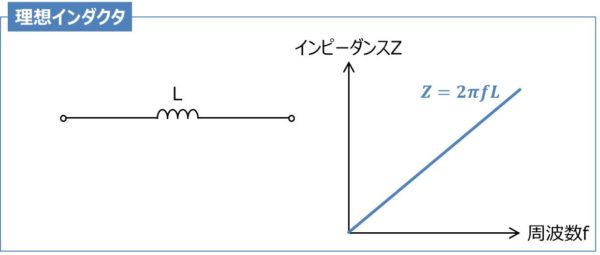
理想のインダクタ(コイル)はインダクタンス以外の成分がないため、Lのみで表されます。そのため、理想のインダクタは周波数が高くなるにつれて、インピーダンスが増加します。
しかし、実際のインダクタはインダクタンス以外に巻線の直流抵抗RDCや線間容量CP等を持っています。そのため、インダクタの等価回路を表す場合、巻線の直流抵抗RDCや線間容量CPを考慮する必要があります。
インダクタの等価回路には大きく5つのモデル(2素子モデル~5素子モデル)があります。
例えば、2素子モデルは巻線の直流抵抗RDCを考慮したモデルであり、3素子モデルは巻線の直流抵抗RDCと線間容量CPを考慮したモデルとなっています。
では、これから各モデルを順番に説明していきます。
インダクタの等価回路(2素子モデル)
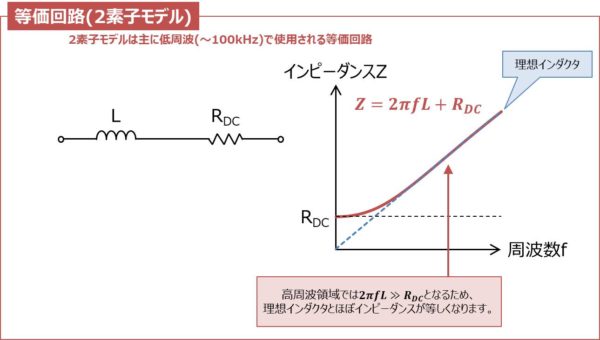
上図はインダクタの等価回路(2素子モデル)と周波数特性です。
2素子モデルは主に低周波(~100kHz)で使用される等価回路です。
Lはインダクタのインダクタンスを、RDCはインダクタの巻線の直流抵抗を表しています。高周波領域では\(2{\pi}fL{\gg}R{DC}\)となるので、理想インダクタとほぼインピーダンスが等しくなります。
この2素子モデルは最も分かりやすいインダクタの等価回路となっています。
補足
インダクタの等価回路(3素子モデル)
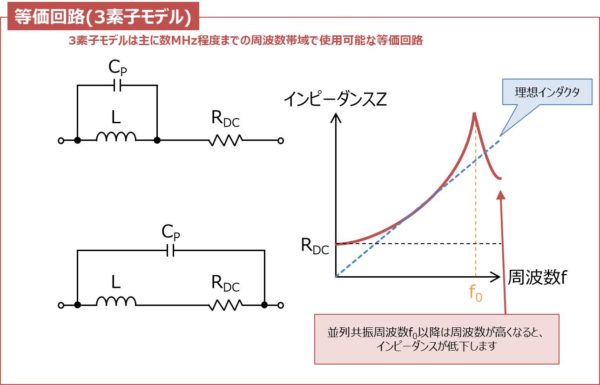
上図はインダクタの等価回路(3素子モデル)と周波数特性です。
3素子モデルは主に数MHz程度までの周波数帯域で使用可能な等価回路です。
3素子モデルはインダクタの等価回路としては最も一般的なモデルとなっており、2素子モデルに対して線間容量CPが追加されています。
Lはインダクタのインダクタンスを、RDCはインダクタの巻線の直流抵抗を、CPは線間容量を表しています。線間容量CPは微小な値なので低周波では問題にはなりませんが、高周波では配慮は必要となります。
インダクタの巻線の直流抵抗RDCの位置がサイトやネットによって異なります。LとCPを並列接続したものにRDCを直列に接続した等価回路と、LとRDCを直列接続したものにCPを並列に接続した等価回路がありますが、ほぼ同等の特性となります。
インダクタのインピーダンス特性においてインピーダンスの変曲点となる周波数f0のことを並列共振周波数と呼びます(自己共振周波数と呼ぶ場合もあります)。並列共振周波数f0までは周波数が高くなるにつれてインピーダンスが増加します。一方、並列共振周波数f0以降では周波数が高くなると、インピーダンスが低下するためインダクタとしての機能がなくなります。
そのため、インダクタを高周波で使用する場合には仕様書やデータシートで並列共振周波数f0を確認してください。
なお、並列共振周波数f0は以下の式で表されます。
\begin{eqnarray}
f_0=\frac{1}{2{\pi}\sqrt{LC_P}}
\end{eqnarray}
補足
- インダクタはコア材に導線を巻いて作られてるため、巻線の線間容量CPが発生します。もう少し厳密に説明すると、巻線はウレタン等の被膜(絶縁物)で絶縁されています。巻線が絶縁物を挟んでおり、コンデンサと同じ構造になることから線間容量CPが発生します。この線間容量CPによって並列共振周波数f0が発生します。
- 線間容量CPはインダクタの形状(トロイダルやコイル等)によって特性が異なります。
- 巻数が増えると、巻線間のコンデンサが増えるため、線間容量CPが大きくなります。
- 線間容量CPはインダクタのインピーダンス特性において並列共振周波数f0から求めることができます。並列共振周波数をf0、インダクタンスをLとした時に線間容量CPは以下の式で表されます。
\begin{eqnarray}
C_P=\frac{1}{4{\pi}^2{f_0}^2L}
\end{eqnarray} - 並列共振周波数f0では、本来のインダクタンスに対してインピーダンスが増加します。これは並列共振周波数f0では、見かけ上のインダクタンスが大きくなることを意味しています。
インダクタの等価回路(4素子モデル)
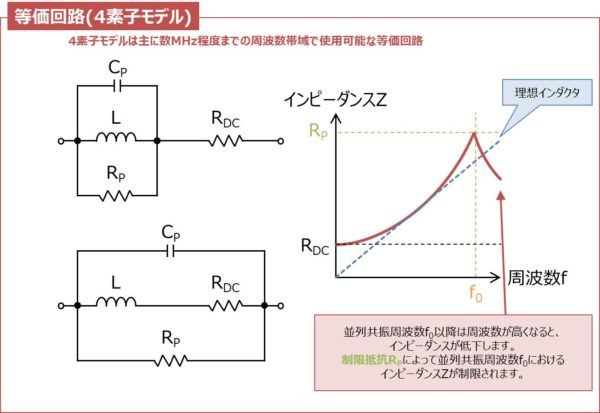
上図はインダクタの等価回路(4素子モデル)と周波数特性です。
4素子モデルは主に数MHz程度までの周波数帯域で使用可能な等価回路です。
3素子モデルに対して制限抵抗RPが追加されています。
Lはインダクタのインダクタンスを、RDCはインダクタの巻線の直流抵抗を、CPは線間容量を、RPはインダクタの共振点におけるインピーダンスを制限するための制限抵抗を表しています。
インダクタの巻線の抵抗Rの位置がサイトやネットによって異なります。LとCPとRPを並列接続したものにRDCを直列に接続した等価回路と、LとRDCを直列接続したものにCPとRPを並列に接続した等価回路がありますが、ほぼ同等の特性となります。
4素子モデルの等価回路のインピーダンスは以下の式で表されます。
\begin{eqnarray}
Z=\displaystyle\frac{1}{\displaystyle\frac{1}{R_P}+\displaystyle\frac{1}{j{\omega}L}+j{\omega}C}+R_{DC}
\end{eqnarray}
ここで、巻線の直流抵抗RDCは小さいため、最大インピーダンスとなる並列共振周波数の点では省略することができ、以下の式のように簡略化されます。
\begin{eqnarray}
Z&{\approx}&\displaystyle\frac{1}{\displaystyle\frac{1}{R_P}+\displaystyle\frac{1}{j{\omega}L}+j{\omega}C}\\
&=&\displaystyle\frac{1}{\displaystyle\frac{1}{R_P}+j\left({\omega}C -\displaystyle\frac{1}{{\omega}L}\right)}
\end{eqnarray}
上式の絶対値は以下の式となります。
\begin{eqnarray}
|Z|=\displaystyle\frac{1}{\sqrt{\left(\displaystyle\frac{1}{R_P}\right)^2+\left({\omega}C -\displaystyle\frac{1}{{\omega}L}\right)^2}}
\end{eqnarray}
ここで、インピーダンスは\({\omega}C=\displaystyle\frac{1}{{\omega}L}\)の時に最大となり、この時の値はRPになります。すなわち、制限抵抗RPによって並列共振周波数f0におけるインピーダンスが制限されます。
\({\omega}C=\displaystyle\frac{1}{{\omega}L}\)となる並列共振角周波数ωは以下の式となります。
\begin{eqnarray}
{\omega}=\sqrt{\displaystyle\frac{1}{LC_P}}
\end{eqnarray}
ω=2πfなので並列共振周波数f0は以下の式で表すことができます。
\begin{eqnarray}
f_0=\displaystyle\frac{1}{2{\pi}\sqrt{LC_P}}
\end{eqnarray}
インダクタの等価回路(5素子モデル)
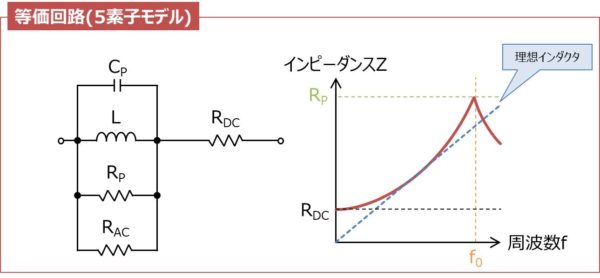
上図はインダクタの等価回路(5素子モデル)と周波数特性です。
5素子モデルはコイルの鉄損(ヒステリシス損と渦電流損)を考慮した等価回路です。RACは主にコアの損失で鉄損と呼ばれるものになります。
【補足】インダクタの等価回路をシミュレーションする
LTspiceでインダクタの各等価回路をシミュレーションしてみます。
インダクタの等価回路(2素子モデル)のシミュレーション
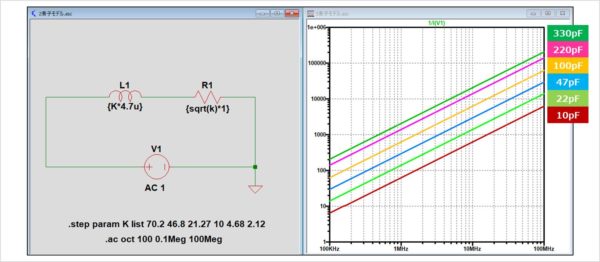
上図のシミュレーションはインダクタンスを変えてシミュレーションを行う回路です。
インダクタンス4.7uH、巻線の直流抵抗1Ωのインダクタに対して変数Kを用いてインダクタンス値と直流抵抗値を変えています。
変数Kは「.step param K list 70.2 46.8 21.27 10 4.68 2.12」というstep文を用いることで変えています。
またシミュレーション結果は「1/I(L1)」で表示しています。信号源の電圧の大きさが「1」なので「1/I(L1)」は「電圧/電流」となり、インピーダンスを表します。
インダクタンスは
- 10uH(4.7uHの約2.12倍)
- 22uH(4.7uHの約4.68倍)
- 47uH(4.7uHの10倍)
- 100uH(4.7uHの約4.68倍)
- 220uH(4.7uHの約46.8倍)
- 330uH(4.7uHの約70.2倍)
の7つでシミュレーションしています。
2素子モデルは周波数が比例してインピーダンスが増加します。これはインダクタのインピーダンスZがZ=ωL=2πfLなので周波数fが高くなるにつれてZが大きくなるからです。
補足
インダクタの等価回路(3素子モデル)のシミュレーション
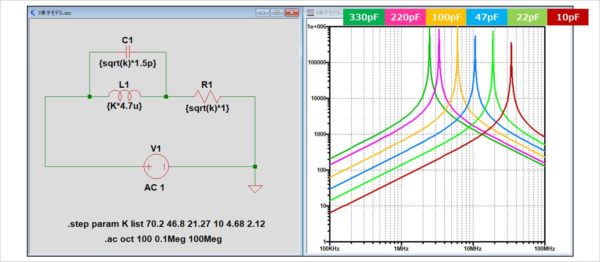
3素子モデルは並列共振周波数f0以降ではインピーダンスが低下します。また、インダクタンスLの値が小さいほど並列共振周波数が高くなるため、インダクタとして働く周波数が広くなります。
インダクタの等価回路(4素子モデル)のシミュレーション
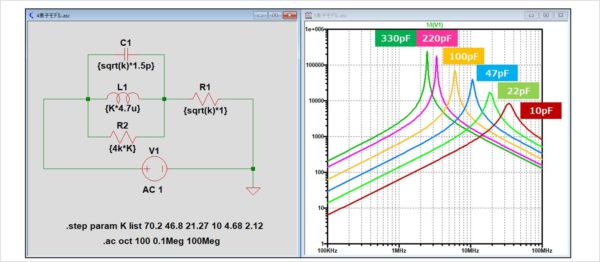
4素子モデルは3素子モデルと同様に、並列共振周波数f0以降ではインピーダンスが低下します。また、インダクタンスLの値が小さいほど並列共振周波数が高くなるため、インダクタとして働く周波数が広くなります。また、3素子モデルに対して制限抵抗を追加したため、並列共振周波数f0におけるインピーダンスが制限されていることも分かります。
まとめ
この記事では『インダクタの等価回路と周波数特性』について、以下の内容を説明しました。
当記事のまとめ
- インダクタの各等価回路の説明と周波数特性
- インダクタの各等価回路のシミュレーション結果
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。






