【ゲート駆動回路】ゲート抵抗と駆動ICの消費電力の式・計算方法

2019年8月11日

ゲート駆動回路において、『駆動ICの消費電力』、『ゲート抵抗の消費電力』、『ゲート駆動回路の消費電力』の式、計算方法について説明します。

ゲート駆動回路の消費電力の式

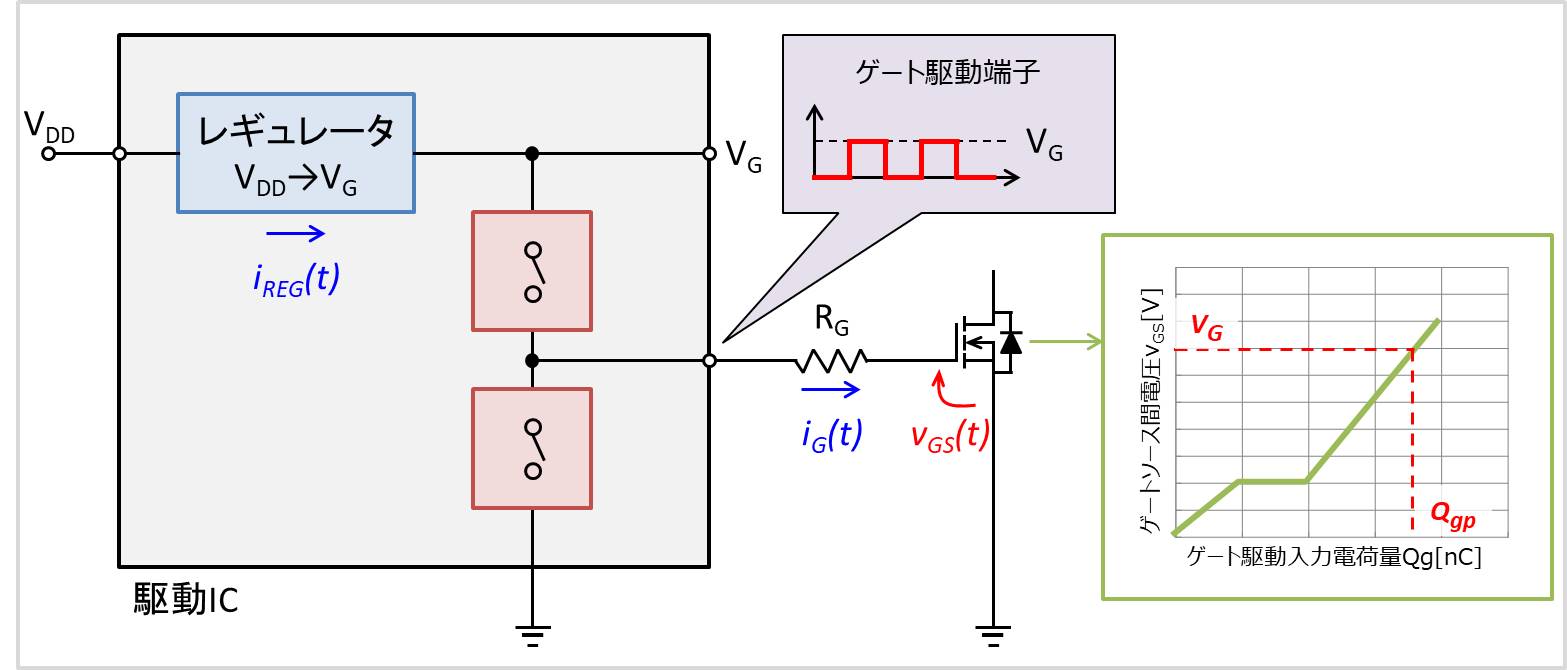
一般的には上図のようにゲート駆動回路は、駆動ICとゲート抵抗R_Gで構成されており、駆動ICのゲート駆動端子はゲート抵抗R_Gを介してMOSFRTのゲート(G)に接続されています。

駆動IC内のスイッチ(トランジスタ等)がON/OFFを行い、ゲート駆動端子の電圧がHigh電圧(図ではV_G)とLow電圧(図では0V)と変化することで、MOSFETを制御しています。

また、駆動ICは外部から入力電圧V_DDが供給されています。

MOSFETのゲート(G)を駆動する方法は大きく2つあります。

入力電圧V_DDをそのままゲート電圧V_Gとして用いる方法。
入力電圧V_DDを駆動IC内のレギュレータで降圧して、ゲート電圧V_Gにしてからゲート駆動に用いる方法(上図の例です)。

駆動ICのゲート駆動端子の電圧がHigh電圧(図ではVG)となると、MOSFETのゲートソース間電圧v_GSが立ち上がります。

ゲートソース間電圧v_GSが0VからV_Gとなるときにゲートに蓄積される電荷量(ゲート入力電荷量)QgがQgpになるとします。

この時、『駆動ICの消費電力P_IC』、『ゲート抵抗の消費電力P_RG』、『ゲート駆動回路の消費電力P_SW』は、

\begin{eqnarray}
P_{IC}&=&Qgp(V_{DD}-V_{G})f_{SW}\\
P_{RG}&=&QgpV_{G}f_{SW}\\
P_{SW}&=&P_{IC}+P_{RG}=QgpV_{DD}f_{SW}
\end{eqnarray}

となります。ここで、f_SWはスイッチング周波数です。

この式より、ゲート入力電荷量Qgpが大きいほど、入力電圧V_DDが高いほど、スイッチング周波数f_SWが早いほど、ゲート駆動回路の消費電力P_SWが大きくなることがわかります。

実際には駆動ICの漏れ電流による消費電力などがあるので、ゲート駆動回路の消費電力はもう少し大きくなります。駆動ICの漏れ電流による消費電力については下記を参照してください。

【ゲート駆動回路】 ICの消費電流によって生じる消費電力

例えば、入力電圧V_DD=10V、ゲート電圧V_G=8V、MOSFETのゲート入力電荷量Qg=30nC、スイッチング周波数f_SW=500kHzとすると、ゲート駆動回路の消費電力P_SWは
\begin{eqnarray}
P_{SW}=QgpV_{DD}f_{SW}=0.15[W]
\end{eqnarray}
となります。

各消費電力の導出方法

上図の回路において『駆動ICの消費電力P_IC』、『ゲート抵抗の消費電力P_RG』、『ゲート駆動回路の消費電力P_SW』が、
\begin{eqnarray}
P_{IC}&=&Qgp(V_{DD}-V_{G})f_{SW}\\
P_{RG}&=&QgpV_{G}f_{SW}\\
P_{SW}&=&P_{IC}+P_{RG}=QgpV_{DD}f_{SW}
\end{eqnarray}
となる理由を求めます。

まず、上図の回路の原理について説明します。

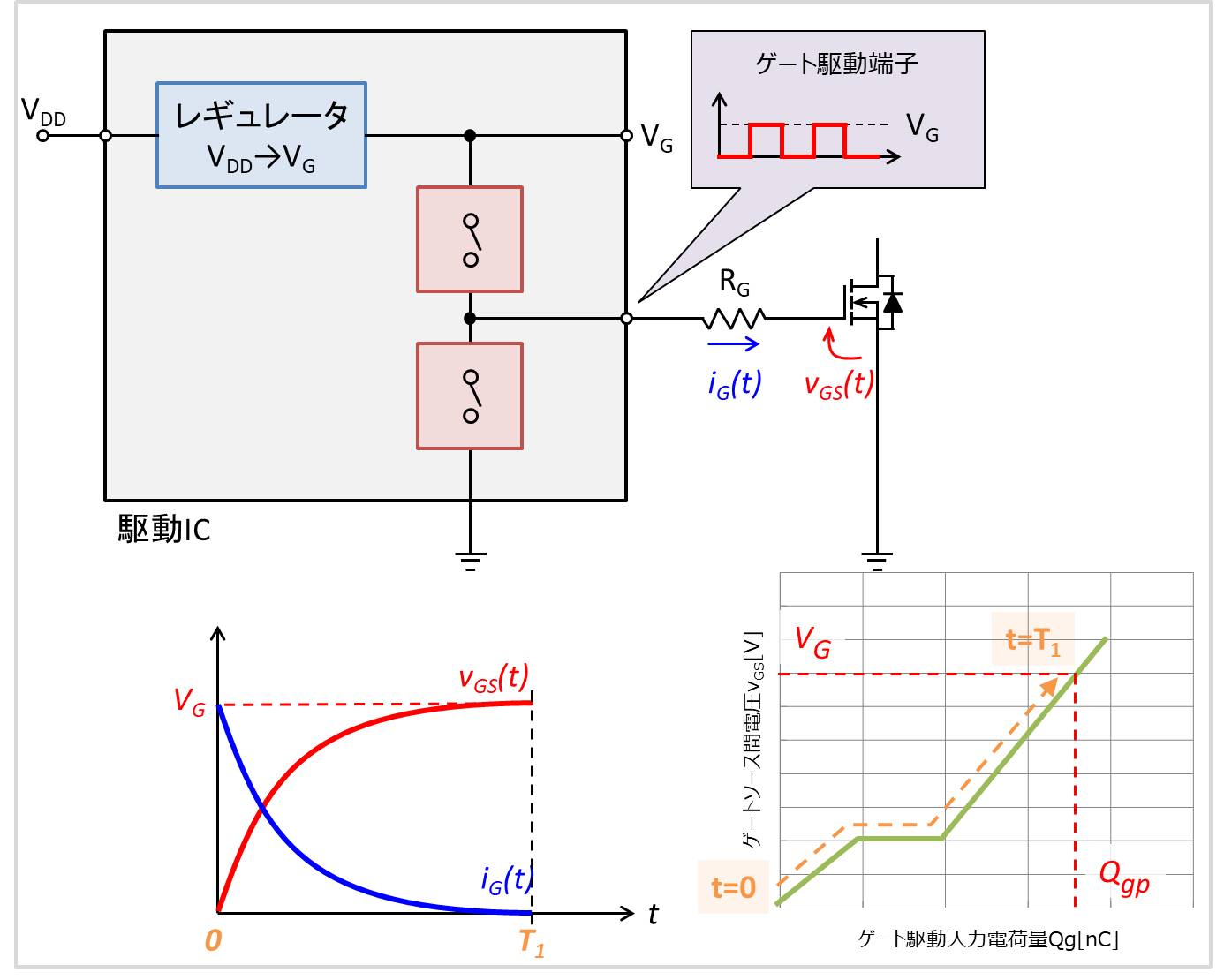
上図では、入力電圧V_DDを駆動IC内のレギュレータで降圧し、ゲート電圧V_Gにしています。ゲート抵抗R_Gに流れるゲート電流をi_G(t)、ゲートソース間電圧をv_GS(t)、ゲートソース間電圧v_GS(t)が0VからV_Gになった時のゲート入力電荷量QgをQgpとしています。

t＝0において、駆動IC内のハイサイドスイッチがオンすると、ゲート電流i_Gが流れ、MOSFETのゲートに電荷が溜まります。
t=T₁でゲートソース間電圧v_GSの電圧がV_G、ゲート電流i_Gが0、ゲート入力電荷量QgがQgpになったとします。

なお、これから各消費電力を求める上で以下の式を用います。
\begin{eqnarray}
Qg=\displaystyle \int i_{G}(t)dt{\hspace{ 10pt }}{\Leftrightarrow}{\hspace{ 10pt }}i_{G}(t)=\displaystyle\frac{dQg}{dt}
\end{eqnarray}
これは、ゲート入力電荷量Qgはゲート電流i_G(t)を時間で積分すると求めることを示している式です。

駆動ICの消費電力

駆動IC内のハイサイドスイッチがオンしている間、駆動IC内のレギュレータには、V_DD -V_Gの電圧が印加されており、電流i_G(t)が流れています。したがって、オン時において、駆動ICの消費エネルギーE_ICは
\begin{eqnarray}
E_{IC}=\displaystyle \int_{0}^{T_1}(V_{DD}-V_{G})i_{G}(t)dt
\end{eqnarray}
となります。
ここで、\(t：0{\to}T_1\)において、\(Qg：0{\to}Qgp\)であり、
\begin{eqnarray}
i_{G}(t)=\displaystyle\frac{dQg}{dt}
\end{eqnarray}
なので、上式を計算すると、
\begin{eqnarray}
E_{IC}&=&\displaystyle \int_{0}^{Qgp}(V_{DD}-V_{G})\displaystyle\frac{dQg}{dt}dt\\
&=&Qgp(V_{DD}-V_{G})
\end{eqnarray}

なります。上式は駆動IC内のハイサイドスイッチのオン1回における消費エネルギーE_ICです。これにスイッチング周波数f_SWをかけることで、駆動ICの消費電力P_ICを求めることができ、

\begin{eqnarray}
P_{IC}&=&Qgp(V_{DD}-V_{G})f_{SW}
\end{eqnarray}

となります。

ゲート抵抗の消費電力の求め方

駆動IC内のハイサイドスイッチがオンしている間、駆動ICのゲート駆動端子から供給されるエネルギーE_ICGは、
\begin{eqnarray}
E_{ICG}=\displaystyle \int_{0}^{T_1}V_{G}i_{G}(t)dt
\end{eqnarray}
となります。
ここで、\(t：0{\to}T_1\)において、\(Qg：0{\to}Qgp\)であり、
\begin{eqnarray}
i_{G}(t)=\displaystyle\frac{dQg}{dt}
\end{eqnarray}
なので、上式を計算すると
\begin{eqnarray}
E_{ICG}&=&\displaystyle \int_{0}^{Qgp}V_{G}\displaystyle\frac{dQg}{dt}dt\\
&=&QgpV_G
\end{eqnarray}
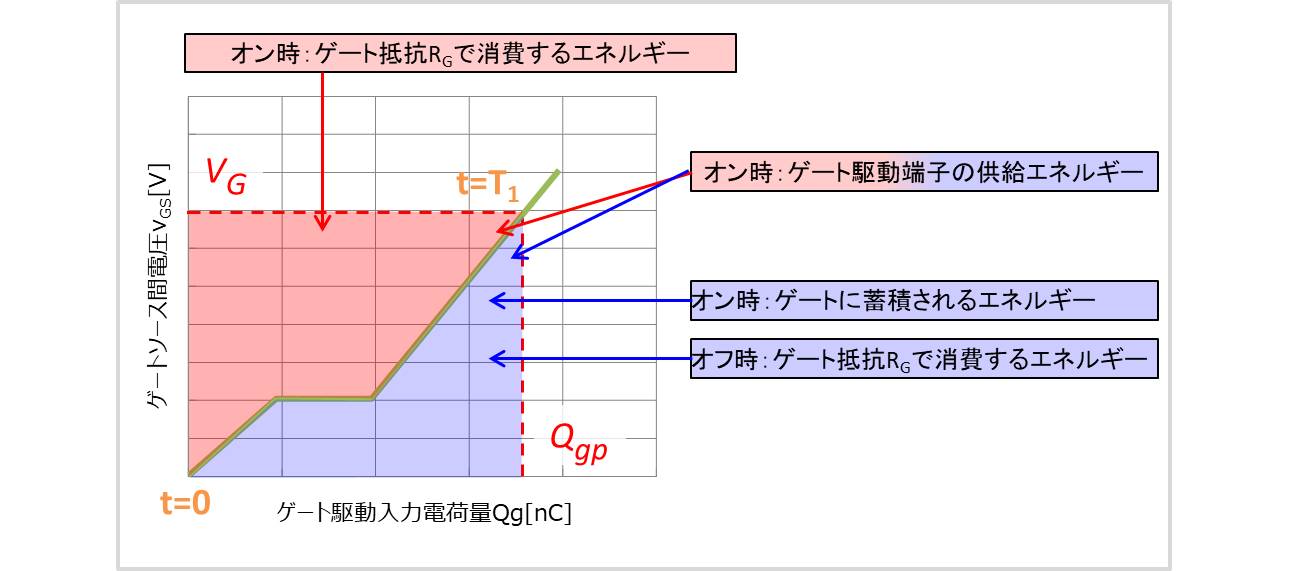
となります。これは、下図の赤の領域と青の領域の合計になります。

また、駆動IC内のハイサイドスイッチがオンしている間、MOSFETのゲートに蓄積されるエネルギーE_Gは
\begin{eqnarray}
E_{G}&=&\displaystyle \int_{0}^{T_1}v_{GS}(t)i_{G}(t)dt\\
&=&\displaystyle \int_{0}^{Qgp}v_{GS}(t)\displaystyle\frac{dQg}{dt}dt\\
&=&\displaystyle \int_{0}^{Qgp}v_{GS}(t)dQg\\
\end{eqnarray}
となります。これは上図の青の領域になります。

ゲート駆動端子からの供給エネルギーE_ICGからゲートに蓄積されるエネルギーE_Gを引くと、ゲート抵抗R_Gで消費されるエネルギーE_RGONを求めることができます。計算すると、オン時におけるゲート抵抗R_Gでの消費エネルギーE_RGONは
\begin{eqnarray}
E_{RGON}=QgpV_G-\displaystyle \int_{0}^{Qgp}v_{GS}(t)dQg
\end{eqnarray}
となります、上図の赤の領域になります。

また、駆動IC内のオフ時、ゲートに蓄積されたエネルギーE_Gがゲート抵抗R_Gで消費されます。したがって、オフ時におけるゲート抵抗R_Gでの消費エネルギーE_RGOFFは
\begin{eqnarray}
E_{RGOFF}=E_{G}=\displaystyle \int_{0}^{Qgp}v_{GS}(t)dQg
\end{eqnarray}
となります。
そのため1回のスイッチングにおいて、ゲート抵抗R_Gで消費されるエネルギーE_RGは
\begin{eqnarray}
E_{RG}&=&E_{RGON}+E_{RGOFF}\\
&=&\left(QgpV_G-\displaystyle \int_{0}^{Qgp}v_{GS}(t)dQg\right)+\left(\displaystyle \int_{0}^{Qgp}v_{GS}(t)dQg\right)\\
&=&QgpV_{G}
&=&E_{ICG}
\end{eqnarray}
となります。ゲート抵抗R_Gの消費エネルギーE_RGはゲート駆動端子から供給されるエネルギーE_ICGに等しくなります。