【電解コンデンサ】リプル電流による『温度上昇』の計算方法

電解コンデンサはリプル電流が流れることによって、温度が上昇します。

この記事では、電解コンデンサの『素子表面の温度上昇』と『素子中心の温度上昇』の計算方法について説明します。

電解コンデンサの『素子表面』の温度上昇

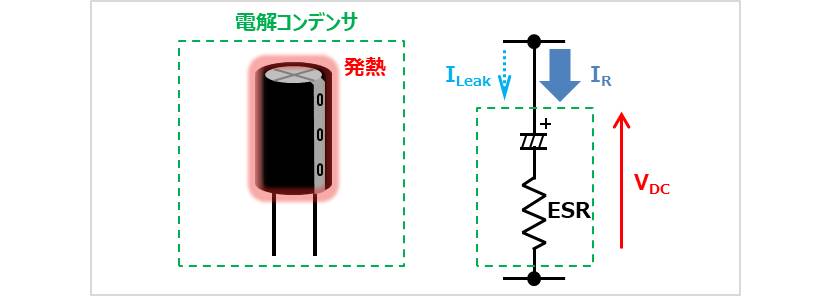
(アルミニウム)電解コンデンサは、他の種類のコンデンサと比較して等価直列抵抗(ESR)が大きいため、損失が大きくなります。そのため、リプル電流I_Rが流れることによってジュール熱が発生し、内部発熱します。

リプル電流による発熱は、電解コンデンサの温度上昇を伴うため、寿命に大きな影響を与えます(電解コンデンサの素子中心の温度が高いほど寿命が短くなる)。

電解コンデンサの消費電力は以下の式で表されます。

\begin{eqnarray}
W&=&W_{R}+W_{Leak}\\
&=&{I_R}^2・ESR+V_{DC}・I_{Leak}
\end{eqnarray}
W:電解コンデンサの消費電力[W]

W_R:リプル電流が流れることによって発生する損失[W]
W_Leak:漏れ電流が流れることによって発生する損失[W]
I_R:リプル電流の実効値[Arms]
ESR:コンデンサの等価直列抵抗(内部抵抗)[Ω]
V_DC:直流電圧(印加電圧)[V]
I_Leak:漏れ電流[A]

直流電圧V_DCが電解コンデンサの定格電圧以下の場合、漏れ電流I_Leakはリプル電流の実効値I_Rよりもはるかに小さい(I_R>>I_Leak)ため、上式は以下の式に変形することができます。

\begin{eqnarray}
W &{\approx}&{I_R}^2・ESR
\end{eqnarray}

ここで、「リプル電流による電解コンデンサの発熱」と「電解コンデンサの表面からの放熱」が平衡になる条件は以下の式となります。

\begin{eqnarray}
{I_R}^2・ESR&=&{\beta}・A・{\Delta}T_S\\
{\Leftrightarrow}{\Delta}T_S &=&\frac{{I_R}^2・ESR}{{\beta}・A }
\end{eqnarray}

β: 放熱定数[10^-3W/℃・cm^2]
A:電解コンデンサのケース表面積[cm^2]
ΔT_S:電解コンデンサの素子表面の温度上昇[℃]

以下にケース径ΦDと放熱定数βの関係表を示します。

このように、放熱定数βはケース径ΦDが大きくなるほど小さな値となり(ケース径が大きいほど放熱能力が高い)、1.5～2.2[10^-3W/℃・cm^2]の範囲となります。

また、ケース表面積Aはケースの直径をΦD、ケースの長さをLとすると以下の式で表されます。

\begin{eqnarray}
A=\frac{\pi}{4}D(D+4{\pi}L)
\end{eqnarray}

さらに、等価直列抵抗ESRは以下の式で与えられます。

\begin{eqnarray}
ESR=\frac{{\tan}{\delta}}{{\omega}C}
\end{eqnarray}

tanδ:損失角の正接
ω:リプル電流の角周波数[rad/s](=2πf)
C:静電容量[F]

以上より、電解コンデンサの素子表面の温度上昇ΔT_Sは以下の式で求めることができます。

\begin{eqnarray}
{\Delta}T_S =\frac{{I_R}^2・ESR}{{\beta}・A}=\frac{{I_R}^2}{{\beta}・A}・\frac{{\tan}{\delta}}{{\omega}C }
\end{eqnarray}

上式より、電解コンデンサの素子表面の温度上昇ΔT_Sはリプル電流I_Rの二乗、等価直列抵抗ESRに比例し、表面積Aに反比例することがわかります。

電解コンデンサの『素子中心』の温度上昇

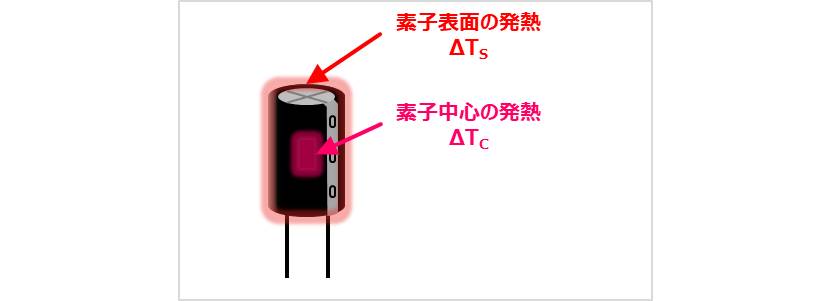
電解コンデンサの素子表面の温度上昇ΔT_Sと素子中心の温度上昇ΔT_Cには温度勾配があり、温度上昇係数αを用いると、以下の式で表すことができます。

\begin{eqnarray}
{\Delta}T_C ={\alpha}{\Delta}T_S
\end{eqnarray}

ΔT_S:電解コンデンサの素子表面の温度上昇
ΔT_C:電解コンデンサの素子中心の温度上昇
α:温度上昇係数(温度差係数)

以下にケース径ΦDと温度上昇係数αの関係表を示します。

温度上昇係数αはケース径ΦDによって異なり、ケース径ΦDが大きくなるほど温度上昇係数αが大きくなります(ケース径ΦDが大きいほど素子中心と素子表面の温度に差があるということ)。

上式より、αは1以上なので、電解コンデンサにリプル電流I_Rが流れることによって生じた自己発熱による温度上昇により、電解コンデンサの素子中心の温度T_Cは素子表面の温度T_Sよりも高くなります。

また、電解コンデンサには寿命があり、時間が経つにつれて、等価直列抵抗ESRが大きくなるため、リプル電流による温度上昇は時間が経つにつれて加速します。

電解コンデンサの素子中心の温度上昇(リプル電流から推測)

先程は、素子表面の温度上昇ΔT_Sを求めた後に、温度上昇係数αを用いて、素子中心の温度上昇ΔT_Cを求めましたが、素子中心の温度上昇ΔT_Cをリプル電流I_Rから推測する方法があります。

電解コンデンサの消費電力Wはリプル電流I_Rの2乗に比例するため、定格リプル電流I_Oを流した時における電解コンデンサの素子中心の温度上昇ΔT_Oと、リプル電流I_Rを流した時における電解コンデンサの素子中心の温度上昇ΔT_Cの関係は以下の式で表されます。

\begin{eqnarray}
\frac{{\Delta}T_C}{{\Delta}T_O}&=&\frac{{I_R}^2}{{I_O}^2}\\
{\Leftrightarrow}{\Delta}T_C&=&{\Delta}T_O×\left(\frac{I_R}{I_O}\right)^2
\end{eqnarray}

ΔT_C:電解コンデンサの素子中心の温度上昇[℃]
ΔT_O:定格リプル電流を流した時における電解コンデンサの素子中心の温度上昇[℃]
I_R:リプル電流の実効値[Arms]
I_O:定格リプル電流[Arms]

ΔT_Oは105℃用基板自立型コンデンサの場合は約5℃となります。また、定格リプル電流I_Oはデータシートに記載されています。

リプル電流の実効値I_Rについて

リプル電流の実効値I_Rは実験で観測したリプル電流の実効値をそのまま用いてはいけません。データシートに記載してある規定周波数に変換した後の値となります。

変換式は以下となっています。

\begin{eqnarray}
R_XI_X^2&=&R_0I_R^2\\
{\Leftrightarrow}I_X&=&\sqrt{\displaystyle\frac{R_O}{R_X}}×I_R=K×I_R\\
{\Leftrightarrow}I_R&=&\displaystyle\frac{I_X}{K}
\end{eqnarray}

I_X:実使用時のリプル電流の実効値[Arms]
I_R:規定周波数におけるリプル電流の実効値[Arms]
K:周波数補正係数

詳しくは以下の記事を参考にしてください。
【電解コンデンサ】リプル電流の『周波数補正係数』とは？