(アルミニウム)電解コンデンサの周波数補正係数とは一言で言えば、『実使用におけるリプル電流』を『規定周波数におけるリプル電流』に変換するための係数となります。
では、この周波数補正係数について詳しく説明します。
電解コンデンサの『周波数補正係数』とは
電解コンデンサの等価直列抵抗ESRは周波数特性を持っています。周波数が高くなるにつれてESRは小さくなります。
ここで、規定周波数f0(一般的には120Hz)におけるESRをR0、リプル電流の実効値をIRとし、周波数fXにおけるESRをRX、リプル電流の実効値をIXとした時、温度上昇が同じになる条件は以下の式となります。
R_XI_X^2&=&R_0I_R^2\\
{\Leftrightarrow}I_X&=&\sqrt{\displaystyle\frac{R_O}{R_X}}×I_R=K×I_R\\
{\Leftrightarrow}I_R&=&\displaystyle\frac{I_X}{K}
\end{eqnarray}
- IX:実使用時のリプル電流の実効値[Arms]
- IR:規定周波数におけるリプル電流の実効値[Arms]
- K:周波数補正係数
この\(\sqrt{\displaystyle\frac{R_O}{R_X}}\)が周波数補正係数Kとなります。周波数補正係数の変数はK以外にもKf、Fなど参考書やネットにより変数名が異なります。また、周波数補正係数Kは定格リプル電流周波数補正係数やリプル電流補正係数とも呼ばれています。
以下に周波数補正係数Kの一例を示します。
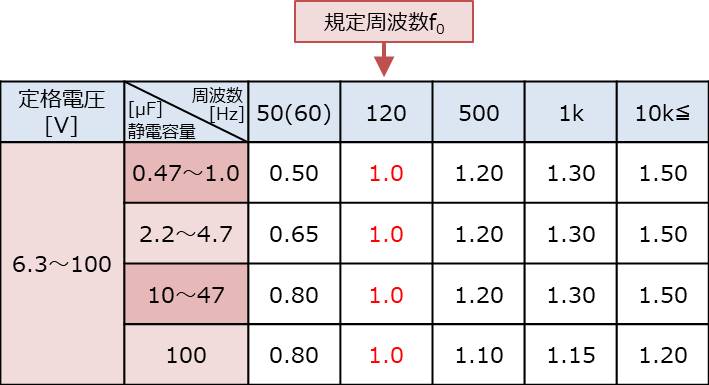
上表において規定周波数f0は1.0になっている周波数となります。上表の場合だと120Hzが規定周波数f0となります。
また、上表より周波数が高くなると、周波数補正係数Kが大きくなっているため、実使用時において流せるリプル電流IXが大きくなります(言い換えると、周波数が高くなるとリプル電流を沢山流しても発熱が少ないということです)。例えば、47uFの電解コンデンサに流れるリプル電流の周波数が50kHzなら、120Hzのリプル電流を流した時と比べて1.5倍の電流を流した時に発熱が同等となります。
補足
複数の周波数を含んだリプル電流の場合
リプル電流に複数の周波数が含まれている時における規定周波数におけるリプル電流IRの計算方法について説明します。
各周波数における周波数補正係数をKN、リプル電流の実効値をIXNとすると、規定周波数におけるリプル電流IRは、
I_R&=&\sqrt{\left(\displaystyle\frac{I_{X1}}{K_1}\right)^2+\left(\displaystyle\frac{I_{X2}}{K_2}\right)^2+…+\left(\displaystyle\frac{I_{XN}}{K_N}\right)^2}
\end{eqnarray}
- IR:規定周波数におけるリプル電流の実効値[Arms]
- IXN:各周波数におけるリプル電流の実効値[Arms]
- KN:各周波数における周波数補正係数
となります。各周波数帯において、規定周波数におけるリプル電流に変換したものの2乗\(\left(\displaystyle\frac{I_{XN}}{K_N}\right)^2\)を足し算し、ルートにしたものとなります。






