【電流の定義】『向き』や『大きさ』や『単位』などを解説！

この記事では、最初に電流とは何なのかを説明します。

その後、

電流の定義(向きと大きさ)
電流の式
電流の単位

などを図を用いて分かりやすく説明しています。

電流とは

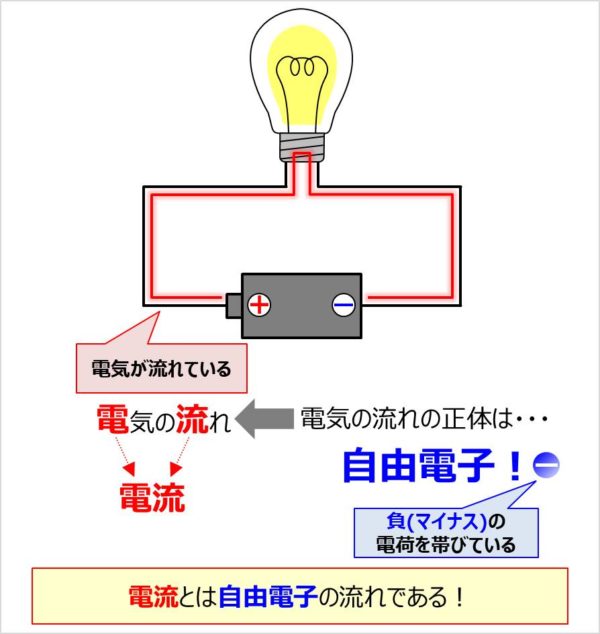
上図のように、豆電球に電池を接続すると、豆電球が光ります。

この時、「豆電球には電気が流れている」とよく言いますよね。また、豆電球以外にも、皆さまが使っている『冷蔵庫などの家電製品』や『スマートフォン』などは全て電気が流れています。

この電気の流れを「電流」と言います。

では、電気の流れとは何でしょうか？「電気」というモノがあって、それが流れているということなのでしょうか？

・・・実は違います。

「電気」というモノはありません。正確に言うと、自由電子という負(マイナス)の電荷を帯びたモノが流れているのです。すなわち、

電流とは自由電子の流れである！

ということになります。

補足

電流は英語ではそのまま「Electric Current」と書きます。「Electric」を省略し、単に「Current」と書くこともあります。

電流の定義

では次に『電流の向きの定義』と『電流の大きさの定義』について説明します。

電流の向き

先ほど、「電流とは自由電子の流れである」と説明しました。

流れには向きがありますよね。例えば、水の場合、高いところから低いところに向かって流れます。

この水と同じように、電流と自由電子の流れにも向きがあります。

この向きについては以下のように定義されています(後ほど詳しく説明します)。

電流の流れる向きは自由電子の流れる向きと逆になる！

もう少し詳しく！

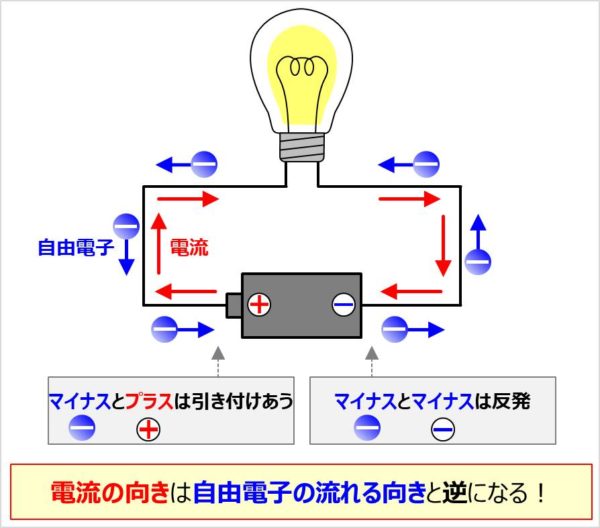
ではこれから、電流の流れる向きについて詳しく説明していきます。

上図は、豆電球に電池を接続しているシンプルな回路です。豆電球に電池を接続することで、電流が流れて、豆電球が光ります。

では、この時、電流の流れる向きはどうなっているのでしょうか。

電流は電池のプラス極からマイナス極に流れます。

一方、自由電子の流れる向きはどうなっているのでしょうか。

自由電子は負(マイナス)の電荷を帯びているため、

マイナスの自由電子と電池のプラス極

→磁石のS極とN極のように引き付けあう。

マイナスの自由電子と電池のマイナス極

→磁石のS極とS極のように反発する。

となります。すなわち・・・

自由電子は電池のマイナス極からプラス極に流れます。

つまり、まとめると、

電流の流れる向きは自由電子の流れる向きと逆になる！

ということが分かります。でも、電流の流れる向きと自由電子の流れる向きが逆向きって分かりにくいですよね。

ここで、マイナスの自由電子ではなく、疑似的なプラスの正電荷で考えると電流の流れる向きと同じになります。

そのため、参考書等を見ると分かりやすく、「電流の流れる向きは正電荷の流れる向きと同じである」と説明している場合もあります。

補足

電池のプラス極は正極とも呼ばれています。
電池のマイナス極は負極とも呼ばれています。

電流の大きさ

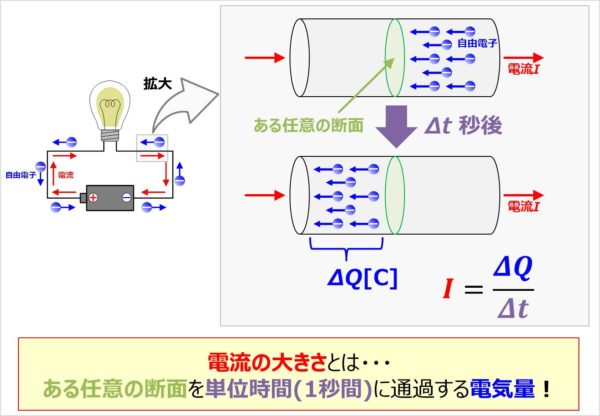
何回も繰り返しになりますが、「電流とは自由電子の流れである」と説明しました。

流れには大きさ(強さ)がありますよね。例えば、水の場合、流れが速かったり、水量が多い場合には水の流れが強くなりますね。

この水と同じように、電流にも大きさがあります。

この電流の大きさついては以下のように定義されています(後ほど詳しく説明します)。

ある任意の断面を単位時間(1秒間)に通過する電気量である！

式で表すと、ある任意の断面をΔt[s]の間にΔQ[C]の電荷が通過する場合、電流の大きさI[A]は次式となります。

\begin{eqnarray}
I=\frac{{\Delta}Q}{{\Delta}t}
\end{eqnarray}

例えば、1秒間(t=1[s])に1Cの電荷(Q=1[C])が通過すれば、電流の大きさは

\begin{eqnarray}
I=\frac{{\Delta}Q}{{\Delta}t}=\frac{1{\mathrm{[C]}}}{1{\mathrm{[s]}}}=1{\mathrm{[A]}}
\end{eqnarray}

となります。

同様に、1秒間(t=1[s])に5Cの電荷(Q=5[C])が通過すれば、電流の大きさは

\begin{eqnarray}
I=\frac{{\Delta}Q}{{\Delta}t}=\frac{5{\mathrm{[C]}}}{1{\mathrm{[s]}}}=5{\mathrm{[A]}}
\end{eqnarray}

となります。

式だと簡単なような気がしますが、少しイメージがしにくいですね。ではこれから、電流の大きさの定義について分かりやすく説明していきます。

もう少し分かりやすく！

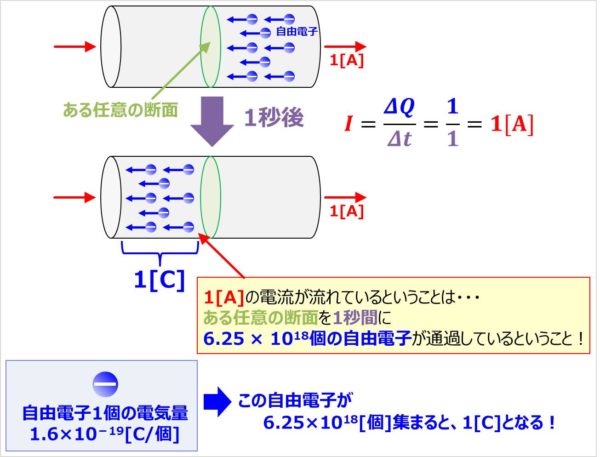
ここで分かりやすく、電流の大きさが1[A]の時に自由電子がどのようになっているのか考えてみましょう。

ある任意の断面を1秒間(t=1[s])に1Cの電荷(Q=1[C])が通過すると、電流の大きさが1[A]となります。

ここで、自由電子1個の電気量は1.6×10^-19[C]です。-19乗なのでとてつもなく小さいですね。この自由電子が
\begin{eqnarray}
\frac{1{\mathrm{[C]}}}{1.6×10^{-19}{\mathrm{[C/個]}}}=6.25×10^{18}{\mathrm{[個]}}
\end{eqnarray}

集まることで、1[C]となります。

つまり、

1[A]の電流が流れているということは、ある任意の断面を1秒間に6.25×10¹⁸個の自由電子が通過している。

ということになります。なんとなく電流の大きさと自由電子のイメージがつかめましたでしょうか。

この自由電子が速く流れる場合や、この自由電子の量が多い場合には、ある任意の断面を1秒間に通過する自由電子の数が多くなるため、電流の大きさが大きくなります。

補足