【コンダクタンスとは】『単位』や『計算方法』などのまとめ！

抵抗Rは「直流回路または交流回路における電流の流れにくさ」を表します。

一方、コンダクタンスGは「直流回路または交流回路における電流の流れやすさ」を表すものです。この記事ではこのコンダクタンスについて

コンダクタンスとは
コンダクタンスの特徴
合成コンダクタンスの計算方法
コンダクタンスの計算例

などを図を用いて分かりやすく説明しています。

コンダクタンスとは

最初にコンダクタンスの要点を以下にまとめます。

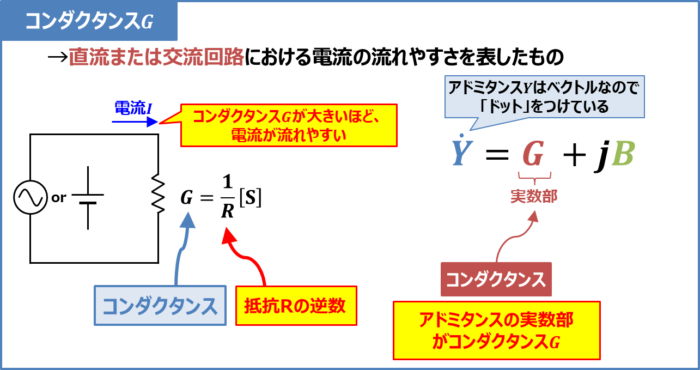
コンダクタンスの要点

コンダクタンスは抵抗Rの逆数であり、記号はG、単位は[S]である
コンダクタンスは大きいほど電流が流れやすくなる
コンダクタンスはアドミタンス(Y=G+jB)の実数部である

各要点について順番に説明します。

コンダクタンスは抵抗Rの逆数であり、記号はG、単位は[S]である

コンダクタンスは「直流回路または交流回路における電流の流れやすさ」を表し、抵抗Rの逆数となります。記号はG、単位は[S](ジーメンス)を用います。式で表すと次式となります。

\begin{eqnarray}
G=\frac{1}{R}{\mathrm{[S]}}\tag{1}
\end{eqnarray}

例えば、10[Ω]の抵抗は0.1[S]のコンダクタンスと表現することができます。

ここで、抵抗R[Ω]、電圧V[V]、電流I[A]はオームの法則より以下の関係式があります。

\begin{eqnarray}
I&=&\frac{V}{R}{\mathrm{[A]}}\tag{2}\\
\\
V&=&RI{\mathrm{[V]}}\tag{3}\\
\\
R&=&\frac{V}{I}{\mathrm{[{\Omega}]}}\tag{4}\\
\end{eqnarray}

ここで、(1)式を(2)～(4)式に代入すると、オームの法則における「抵抗R、電圧V、電流I」の関係を「コンダクタンスG、電圧V、電流I」の関係に置き換えることができ、次式となります。

\begin{eqnarray}
I&=&\frac{V}{R}=GV{\mathrm{[A]}}\tag{5}\\
\\
V&=&RI=\frac{I}{G}{\mathrm{[V]}}\tag{6}\\
\\
G&=&\frac{I}{V}{\mathrm{[{\Omega}]}}\tag{7}\\
\end{eqnarray}

そのため、コンダクタンスG[S]と電圧V[V]が分かれば電流I[A]を求めることができ、コンダクタンスG[S]と電流I[A]が分かれば電圧V[V]を求めることができます。

コンダクタンスGは大きいほど、電流が流れやすくなる

抵抗Rは電流の流れにくさを表しています。そのため、抵抗Rの大きさにより電流Iは以下のように変わります。

抵抗Rが大きい

→電流Iが流れにくい

抵抗Rが小さい

→電流Iが流れやすい

一方、コンダクタンスGは抵抗Rの逆数なので、電流の流れやすさを表しています。そのため、コンダクタンスGの大きさにより電流Iは以下のように変わります。

コンダクタンスGが大きい

→電流Iが流れやすい

コンダクタンスGが小さい

→電流Iが流れにくい

また、(5)式ではコンダクタンスG[S]と電圧V[V]が分かっている時、流れる電流I[A]は「\(I=GV{\mathrm{[A]}}\)」であることを説明しました。(5)式よりコンダクタンスGが大きくなると、電流Iが大きくなることが分かりますね。

コンダクタンスはアドミタンスの実数部である

アドミタンスYはコンダクタンスGとサセプタンスBを用いると次式で表されます。

\begin{eqnarray}
{\dot{Y}}=G+jB\tag{8}
\end{eqnarray}

上式より、コンダクタンスGはアドミタンスの実数部であることが分かります。なお、コンダクタンスは『ゼロ』または『正の値』となります。抵抗が接続されていない場合はゼロとなり、抵抗が接続されている場合は抵抗の逆数(正の値)となります。

一方、サセプタンスBは『ゼロ』または『正の値』または『負の値』となります。回路にコンデンサやコイルが接続されていない場合はゼロとなります。また、回路が容量性の場合(コンデンサが接続されている回路)は正の値となり、回路が誘導性の場合(コイルが接続されている回路)は負の値となります。

また、インピーダンスZは次式で表されます。

\begin{eqnarray}
{\dot{Z}}=R+jX\tag{9}
\end{eqnarray}

そのため、(1)式と(8)式と(9)式を用いると次式となります。

\begin{eqnarray}
{\dot{Y}}=\frac{1}{{\dot{Z}}}=G+jB+\frac{1}{R+jX}\tag{10}
\end{eqnarray}

分母を有利化すると、次式に変形することができます。

\begin{eqnarray}
{\dot{Y}}=G+jB&=&\frac{1}{R+jX}\\
&=&\frac{R-jX}{(R+jX)(R-jX)}\\
&=&\frac{R-jX}{R^2+X^2}\\
&=&\frac{R}{R^2+X^2}-j\frac{X}{R^2+X^2}\tag{11}
\end{eqnarray}

すなわち、コンダクタンスGは抵抗RとリアクタンスXを用いると次式となります。

\begin{eqnarray}
G=\frac{R}{R^2+X^2}\tag{12}
\end{eqnarray}

上式において、リアクタンスXがゼロの時は下記のようになり、(1)式と等しくなることが分かります。

\begin{eqnarray}
G=\frac{R}{R^2+X^2}=\frac{R}{R^2+0^2}=\frac{1}{R}\tag{13}
\end{eqnarray}

合成コンダクタンスの計算方法

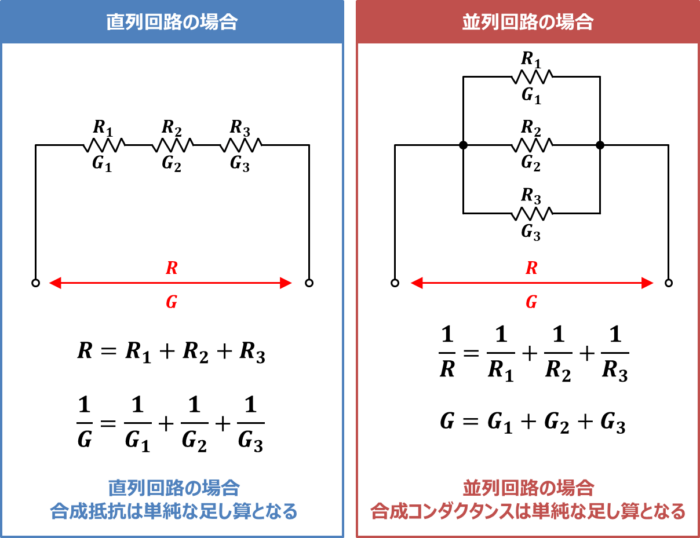
コンダクタンスGを用いる理由は「並列回路の計算が簡単になるから」です。一例として、上図の抵抗R₁,R₂,R₃で構成された直列回路と並列回路において、合成抵抗Rと合成コンダクタンスGを計算してみましょう。

なお、合成抵抗とは「複数の抵抗を1つにみなしたもの」、合成コンダクタンスとは「複数のコンダクタンスを1つに見なしたもの」となります。

直列回路の合成抵抗Rと合成コンダクタンスG

直列回路の場合、合成抵抗Rは以下のように求めます。

\begin{eqnarray}
R={R_1}+{R_2}+{R_3}
\end{eqnarray}

一方、合成コンダクタンスGは以下のように求めます。

\begin{eqnarray}
\frac{1}{G}&=&\frac{1}{G_1}+\frac{1}{G_2}+\frac{1}{G_3}\\
{\Leftrightarrow}G&=&\frac{1}{\displaystyle\frac{1}{G_1}+\displaystyle\frac{1}{G_2}+\displaystyle\frac{1}{G_3}}\
\end{eqnarray}

このように直列回路の場合、合成抵抗Rは単純な足し算で計算することができますが、合成コンダクタンスGは各々のコンダクタンスの逆数の和が合成コンダクタンスの逆数になるため、計算が少し複雑になります。

並列回路の合成抵抗Rと合成コンダクタンスG

並列回路の場合、合成抵抗Rは以下のように求めます。

\begin{eqnarray}
\frac{1}{R}&=&\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}\\
{\Leftrightarrow}R&=&\frac{1}{\displaystyle\frac{1}{R_1}+\displaystyle\frac{1}{R_2}+\displaystyle\frac{1}{R_3}}
\end{eqnarray}

一方、合成コンダクタンスGは以下のように求めます。

\begin{eqnarray}
G={G_1}+{G_2}+{G_3}
\end{eqnarray}

このように並列回路の場合、合成コンダクタンスGは単純な足し算で計算することができますが、合成抵抗Rは各々の抵抗の逆数の和が合成抵抗の逆数になるため、計算が少し複雑になります。

したがって、並列回路の計算ではコンダクタンスを用いる方が簡単になります。一例として次に簡単な例題を用意したので解いてみましょう。

コンダクタンスの計算例

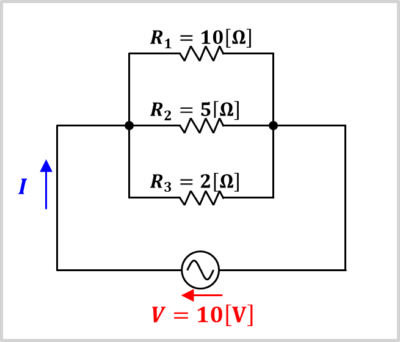
一例として、上図の抵抗R₁,R₂,R₃で構成された並列回路に流れる電流を求めてみましょう。以下の2つの方法で流れる電流Iを求めます。各々の計算方法を見ると、コンダクタンスを用いる方法が一番簡単なのが分かります。

【計算例①】抵抗のまま計算する方法
【計算例②】抵抗をコンダクタンスに変換して計算する方法

【計算例①】抵抗のまま計算する方法

合成抵抗Rは以下の値となります。

\begin{eqnarray}
R&=&\frac{1}{\displaystyle\frac{1}{R_1}+\displaystyle\frac{1}{R_2}+\displaystyle\frac{1}{R_3}}\\
&=&\frac{1}{\displaystyle\frac{1}{10}+\displaystyle\frac{1}{5}+\displaystyle\frac{1}{2}}\\
&=&\frac{10}{1+2+5}\\
&=&\frac{10}{8}{\mathrm{[{\Omega}]}}
\end{eqnarray}

したがって、回路に流れる電流Iは以下の値となります。

\begin{eqnarray}
I&=&\frac{V}{R}=\frac{10}{\displaystyle\frac{10}{8}}=8{\mathrm{[A]}}
\end{eqnarray}

【計算例①】抵抗をコンダクタンスに変換して計算する方法

合成コンダクタンスGは以下の値となります。

\begin{eqnarray}
G&=&{G_1}+{G_2}+{G_3}\\
&=&\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}\\
&=&\frac{1}{10}+\frac{1}{5}+\frac{1}{2}\\
&=&0.1+0.2+0.5\\
&=&0.8{\mathrm{[S]}}
\end{eqnarray}

したがって、回路に流れる電流Iは以下の値となります。

\begin{eqnarray}
I=GV=0.8×10=8{\mathrm{[A]}}
\end{eqnarray}

まとめ

この記事では『コンダクタンス』について、以下の内容を説明しました。