【昇圧コンバータの設計】『出力電流』の導出

この記事では『昇圧コンバータ』において

昇圧コンバータの『出力電流I_OUT』の導出方法

などを図を用いて分かりやすく説明しています。

昇圧コンバータの『出力電流』

昇圧コンバータ(ブーストコンバータ、ステップ・アップ・コンバータ、昇圧チョッパとも呼ばれます)の出力電流\(I_{OUT}\)は一般的には設計時に決定しますが、『入力電力\(P_{IN}\)・出力電力\(P_{OUT}\)・出力電圧\(V_{OUT}\)・効率\({\eta}\)』から導出することもできます。また、『インダクタンス\(L\)・インダクタ電流\(i_{L}\)の最大値\(I_{L(MAX)}\)、最小値\(I_{L(MIN)}\)・スイッチング周波数\(f_{SW}\)等』から導出することもできます。

各導出方法における出力電流\(I_{OUT}\)の式を以下に示します。

『入力電力\(P_{IN}\)・出力電力\(P_{OUT}\)・出力電圧\(V_{OUT}\)・効率等』から導出
\begin{eqnarray}
I_{OUT}={\eta}×\frac{P_{IN}}{V_{OUT}}={\eta}×\frac{V_{IN}I_{IN}}{V_{OUT}}
\end{eqnarray}

インダクタンス\(L\)・インダクタ電流\(i_{L}\)の最大値\(I_{L(MAX)}\)、最小値\(I_{L(MIN)}\)・スイッチング周波数\(f_{SW}\)等』から導出
\begin{eqnarray}
I_{OUT}=\frac{L×f_{SW}×{\eta}×({I_{L(MAX)}}^2-{I_{L(MIN)}}^2)}{2×V_{OUT}×D}
\end{eqnarray}

これら式を導出します。

入力電力・出力電力・出力電圧・効率等から導出

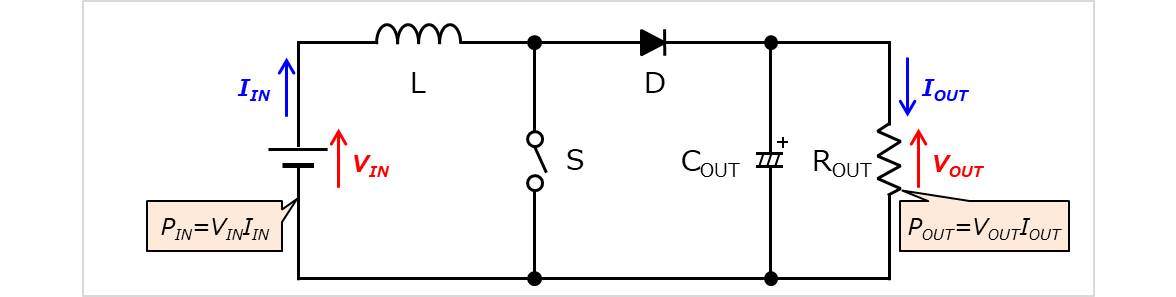
昇圧コンバータにおいて、『入力電力\(P_{IN}\)・出力電力\(P_{OUT}\)・出力電圧\(V_{OUT}\)・効率\({\eta}\)』から出力電流\(I_{OUT}\)を求めます。

効率\({\eta}\)は以下の式で表されます。
\begin{eqnarray}
{\eta}=\frac{P_{OUT}}{P_{IN}}=\frac{V_{OUT}I_{OUT}}{V_{IN}I_{IN}}\tag{1}
\end{eqnarray}
したがって、出力電流\(I_{OUT}\)は
\begin{eqnarray}
I_{OUT}={\eta}×\frac{P_{IN}}{V_{OUT}}={\eta}×\frac{V_{IN}I_{IN}}{V_{OUT}}\tag{2}
\end{eqnarray}
となります。

インダクタンス・インダクタ電流・スイッチング周波数等から導出

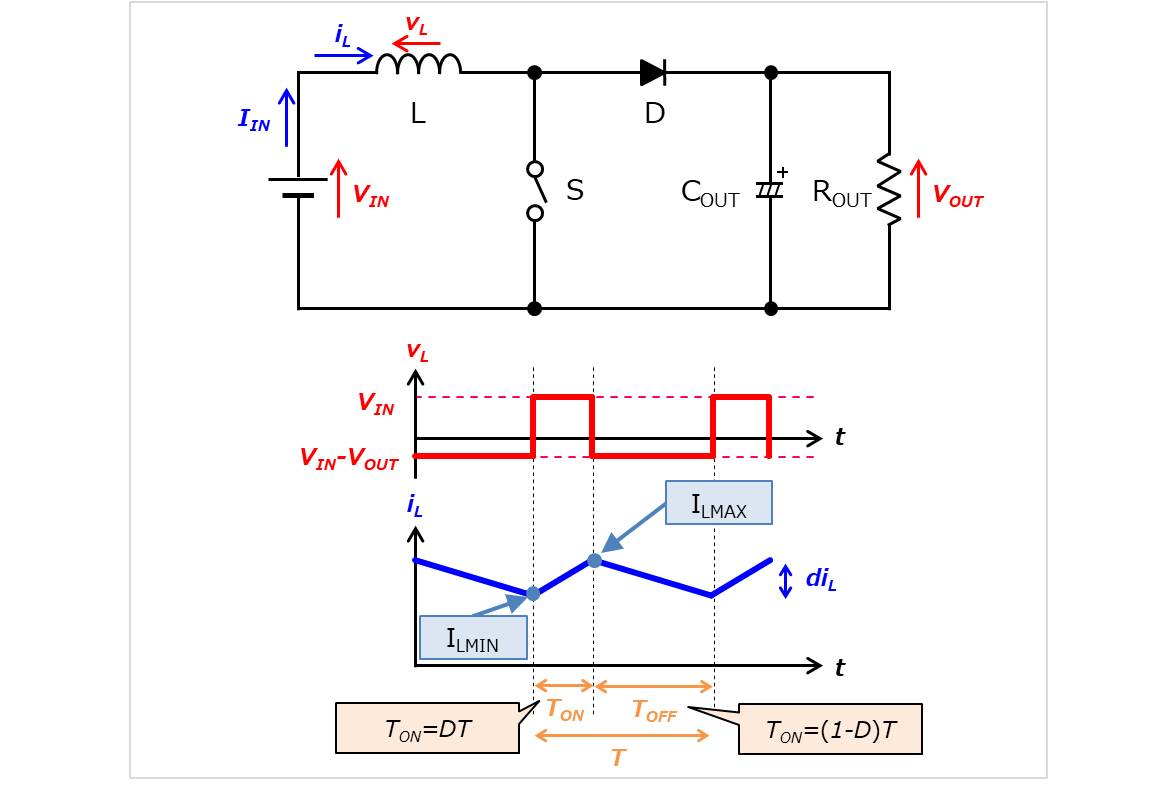
『インダクタンス\(L\)・インダクタ電流\(i_{L}\)の最大値\(I_{L(MAX)}\)、最小値\(I_{L(MIN)}\)・スイッチング周波数\(f_{SW}\)等』から出力電流\(I_{OUT}\)を求めます。

スイッチのオン期間\(T_{ON}\)では、インダクタ電流\(i_{L}\)が最小値\(I_{L(MIN)}\)から最大値\(I_{L(MIN)}\)まで変化します。この時、インダクタ\(L\)には入力電圧\(V_{IN}\)が印可されており、平均電流\(I_{IN}\)が流れているので、以下の式が成り立ちます。
\begin{eqnarray}
\frac{1}{2}L {I_{L(MAX)}}^2-\frac{1}{2}L {I_{L(MIN)}}^2= V_{IN} I_{IN} T_{ON}\tag{3}
\end{eqnarray}

また、効率\({\eta}\)、スイッチのオン期間\(T_{ON}\)、スイッチング周波数\(f_{SW}\)、周期\(T\)の関係式は以下となっています。
\begin{eqnarray}
{\eta}=\frac{P_{OUT}}{P_{IN}}=\frac{V_{OUT}I_{OUT}}{V_{IN}I_{IN}}\tag{4}\\
T_{ON}=D×T=\frac{D}{f_{SW}}\tag{5}
\end{eqnarray}

(4)式と(5)式を用いると、(3)式は以下の式となります。
\begin{eqnarray}
\frac{1}{2}L {I_{L(MAX)}}^2-\frac{1}{2}L {I_{L(MIN)}}^2=\frac{ V_{OUT}I_{OUT}}{{\eta}}×\frac{D}{f_{SW}}\tag{6}
\end{eqnarray}
(6)式の左辺を出力電流\(I_{OUT}\)にすると、以下の式となります。

\begin{eqnarray}
I_{OUT}=\frac{L×f_{SW}×{\eta}×({I_{L(MAX)}}^2-{I_{L(MIN)}}^2)}{2×V_{OUT}×D}\tag{7}
\end{eqnarray}

インダクタンス・インダクタ電流・スイッチング周波数等から導出(その2)

なお、この式はスイッチのオフ期間\(T_{OFF}\)からも導出することができます。

スイッチのオフ期間\(T_{OFF}\)において、インダクタ電流が最大値\(I_{L(MAX)}\)から最小値\(I_{L(MIN)}\)まで変化します。したがって、インダクタの磁気エネルギーは\(\displaystyle\frac{1}{2}L{I_{L(MAX)}}^2\)から\(\displaystyle\frac{1}{2}L{I_{L(MIN)}}^2\)に変化します。

この時、インダクタ\(L\)には入力電圧\(V_{IN}-V_{OUT}\)が印可されており、平均電流\(I_{IN}\)が流れているので、以下の式が成り立ちます。
\begin{eqnarray}
\frac{1}{2}L {I_{L(MIN)}}^2-\frac{1}{2}L {I_{L(MAX)}}^2= (V_{IN}- V_{OUT}) I_{IN} T_{OFF}\tag{8}
\end{eqnarray}
となります。スイッチのオン期間\(T_{ON}\)の時と同様に式変形すると、

\begin{eqnarray}
I_{OUT}=\frac{L×f_{SW}×{\eta}×({I_{L(MAX)}}^2-{I_{L(MIN)}}^2)}{2×V_{OUT}×D}\tag{9}
\end{eqnarray}

となります。