【昇圧コンバータの設計】『オンデューティ比D』の導出

昇圧コンバータ(ブーストコンバータ、ステップ・アップ・コンバータ、昇圧チョッパとも呼ばれます)のオンデューティ比Dの導出方法について説明します。

昇圧コンバータのオンデューティ比D

昇圧コンバータのオンデューティ比\(D\)は、入力電圧を\(V_{IN}\)、出力電圧\(V_{OUT}\)をとすると、以下の式で表されます。

\begin{eqnarray}
D=1-\frac{ V_{IN}}{ V_{OUT}}\tag{1}
\end{eqnarray}

この式を導出します。

インダクタ電流の増加と減少が等しいことを利用した導出

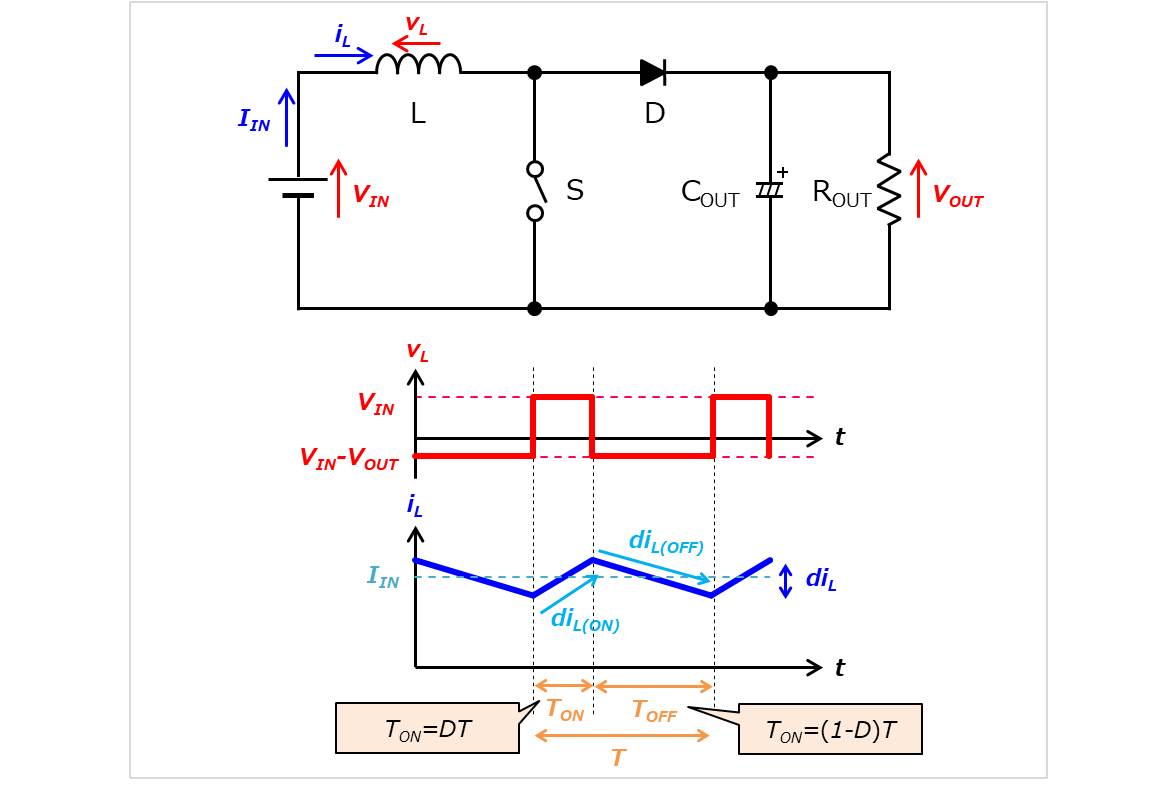
スイッチのオン期間を\(T_{ON}\)、オフ期間を\(T_{OFF}\)とすると、周期\(T\)は以下の式で表すことができます。

\begin{eqnarray}
T= T_{ON}+ T_{OFF}\tag{2}
\end{eqnarray}

また、オンデューティ比\(D\)は1周期\(T\)におけるオン期間\(T_{ON}\)の割合なので、以下の式で表すことができます(\(f_{SW}\)：スイッチング周波数)。

\begin{eqnarray}
D= \frac{T_{ON}}{T}=T_{ON}f_{SW}\tag{3}
\end{eqnarray}

ここで、インダクタ電流\(i_{L}\)とインダクタ電圧\(v_{L}\)の関係式は以下の式となります(\(L\)：インダクタンス)。

\begin{eqnarray}
v_{L}&=& L\frac{di_{L}}{dt}\\
{\Leftrightarrow}di_{L}&=&\frac{v_{L}}{L}dt\tag{4}
\end{eqnarray}

昇圧コンバータでは、スイッチのオン期間\(T_{ON}\)において、インダクタ電流\(i_{L}\)が\(di_{L(ON)}\)増加し、スイッチのオフ期間\(T_{OFF}\)において、インダクタ電流\(i_{L}\)が\(di_{L(OFF)}\)減少します。また、インダクタ電流\(i_{L}\)の増加\(di_{L(ON)}\)と減少\(di_{L(OFF)}\)が等しくなります。これを利用してオンデューティ比\(D\)を計算します。

スイッチのオン期間

インダクタ\(L\)には入力電圧\(V_{IN}\)が印加されています(\(v_{L}=V_{IN}\))。したがって、スイッチのオン期間\(T_{ON}\)におけるインダクタ電流の増加\(di_{ON}\)は(4)式を用いると、

\begin{eqnarray}
di_{L(ON)}=\frac{V_{IN}}{L}T_{ON}\tag{5}
\end{eqnarray}

となります。

スイッチのオフ期間

インダクタ\(L\)には入力電圧\(V_{IN}\)と出力電圧\(V_{OUT}\)の差分\(V_{IN}-V_{OUT}\)が印加されています。したがって、スイッチのオフ期間\(T_{OFF}\)におけるインダクタ電流の減少\(di_{OFF}\)は(4)式を用いると、

\begin{eqnarray}
di_{L(OFF)}\frac{V_{IN}-V_{OUT}}{L}T_{OFF}\tag{6}
\end{eqnarray}

となります。

インダクタ電流の増加と減少が等しいことを利用

オン期間\(T_{ON}\)におけるインダクタ電流の増加\(di_{L(ON)}\)とオフ期間\(T_{OFF}\)におけるインダクタ電流の減少\(di_{L(OFF)}\)は等しいので、(5)式と(6)式を用いると、以下の式となります。

\begin{eqnarray}
\frac{V_{IN}}{L}T_{ON}+\frac{V_{IN}-V_{OUT}}{L}T_{OFF}=0\\
{\Leftrightarrow}{V_{IN}}{T_{ON}}=-(V_{IN}-V_{OUT})T_{OFF}\tag{7}
\end{eqnarray}

となります。(7)式の左辺はオン期間\(T_{ON}\)におけるインダクタ電圧の面積であり、右辺はオフ期間\(T_{OFF}\)におけるインダクタ電圧の面積を表しています。これより、インダクタは電圧時間積が等しいことを表しています。

上式を変形すると、

\begin{eqnarray}
{V_{IN}}{T_{ON}}&=&-(V_{IN}-V_{OUT})T_{OFF}\\
{\Leftrightarrow}{V_{IN}}(T_{ON}+ T_{OFF})&=& V_{OUT} T_{OFF}\\
{\Leftrightarrow}\frac{V_{OUT}}{ V_{IN}}&=&\frac{ T_{ON}+ T_{OFF}}{T_{OFF}}\\
&=&\frac{T}{T_{OFF}}\\
&=&\frac{1}{\cfrac{T_{OFF}}{T}}\\
&=&\frac{1}{\cfrac{T-T_{ON}}{T}}\\
&=&\frac{1}{1-D}\tag{8}
\end{eqnarray}

したがって、

\begin{eqnarray}
D=\frac{V_{OUT}- V_{IN}}{V_{OUT}}=1-\frac{V_{IN}}{V_{OUT}}\tag{9}
\end{eqnarray}

となります。

補足

なお、ダイオードの順方向電圧降下\(V_{F}\)を考慮すると、スイッチのオフ期間\(T_{OFF}\)におけるインダクタ電流\(di_{L}\)の減少\(di_{L(OFF)}\)が

\begin{eqnarray}
di_{L(OFF)}\frac{V_{IN}-(V_{OUT}+V_{F})}{L}T_{OFF}
\end{eqnarray}

となるので、(9)式は以下の式となります。

\begin{eqnarray}
D=\frac{(V_{OUT}+V_{F})- V_{IN}}{V_{OUT}+V_{F}}=1-\frac{V_{IN}}{V_{OUT}+V_{F}}
\end{eqnarray}

インダクタにかかる電圧時間積が0になることを使用した導出

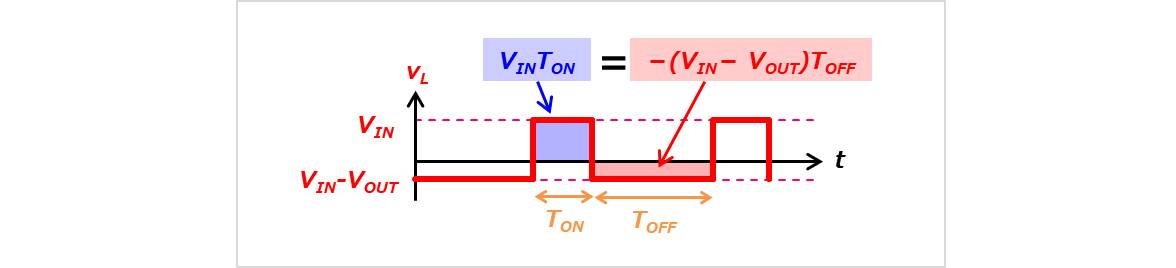
参考種等をみると、インダクタ電圧時間積が0になることを利用して簡潔にオンデューティ比\(D\)を求めている場合が多いです。

上図より、オン期間\(T_{ON}\)でのインダクタ電圧の時間積は\({V_{IN}}{T_{ON}}\)であり、オフ期間\(T_{OFF}\)でのインダクタ電圧の時間積は\(-(V_{IN}-V_{OUT})T_{OFF}\)なので、

\begin{eqnarray}
{V_{IN}}{T_{ON}}=-(V_{IN}-V_{OUT})T_{OFF}\tag{10}
\end{eqnarray}

となります。これは(7)式と同じになり、この後の計算は同様に行います。

インダクタ電流の最大値と最小値、スイッチング周波数を使用した導出

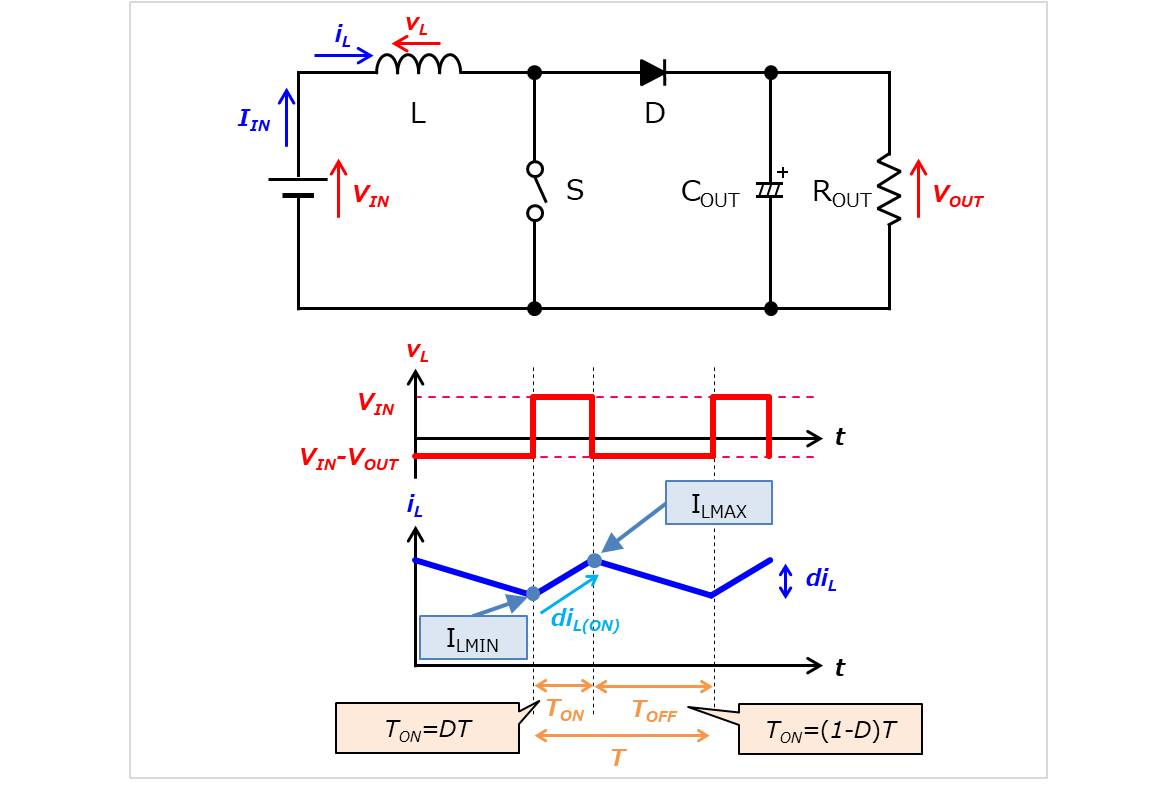
スイッチのオン期間\(T_{ON}\)では、インダクタ\(L\)には入力電圧\(V_{IN}\)が印加されてるため、インダクタ電流\(i_{L}\)は\(di_{L(ON)}\)増加します。ここで、インダクタ電流\(i_{L}\)の最大値を\(I_{L(MAX)}\)、最小値を\(I_{L(MIN)}\)とすると、以下の式となります。

\begin{eqnarray}
V_{IN}=L\frac{di_{L(ON)}}{T_{ON}}=L\frac{I_{L(MAX)}-I_{L(MIN)}}{T_{ON}}\tag{11}
\end{eqnarray}

ここで、(3)式を用いると(11)式は以下の式となります。

\begin{eqnarray}
V_{IN}=L\frac{I_{L(MAX)}-I_{L(MIN)}}{T×D}\tag{12}
\end{eqnarray}

(12)式において、スイッチング周波数\(f_{SW}\)と周期\(T\)の関係式\(T=\displaystyle\frac{1}{f_{SW}}\)を用いると、

\begin{eqnarray}
D&=&L\frac{I_{L(MAX)}-I_{L(MIN)}}{T×V_{IN}}\\
&=&L\frac{f_{SW}(I_{L(MAX)}-I_{L(MIN)})}{V_{IN}}\tag{13}
\end{eqnarray}

となります。