昇圧コンバータは軽負荷時(出力電流が小さい時)、インダクタ電流が不連続モードで動作し、重負荷時(出力電流が大きい時)、連続モードで動作します。この連続モードと不連続モードが切り替わる境界を臨界モードと呼びます。臨界モードでは、インダクタ電流のリプルの最小値が0Aとなります。
これから、連続モードと不連続モードの境界条件(臨界モードで動作する条件)について説明します。
連続モードと不連続モードの境界条件の導出
連続モードと不連続モードの境界条件(臨界モードで動作する条件)になる出力電流\(I_{OUT}\)は以下の式となります。
I_{OUT}=\frac{( V_{OUT}-V_{IN})×{V_{IN}}^2×{\eta}}{2×{V_{OUT}}^2×f_{SW}×L}
\end{eqnarray}
これから、上式の導出方法について説明します。
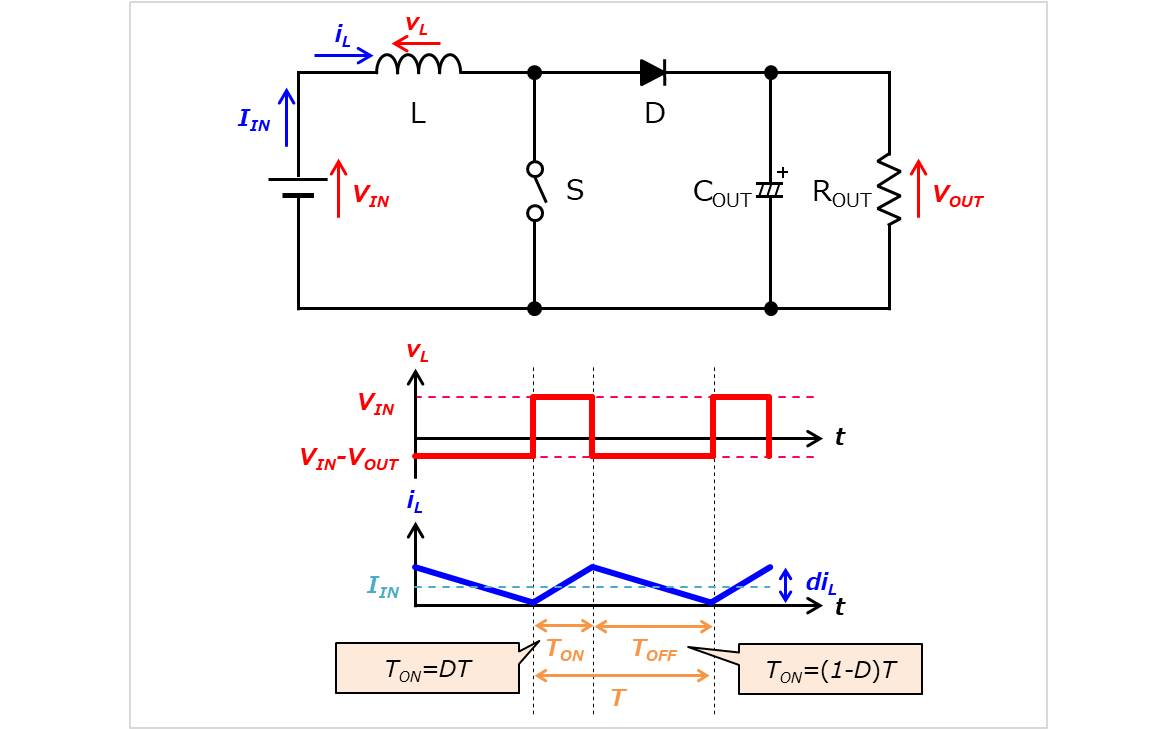
スイッチのオン期間\(T_{ON}\)では、インダクタ\(L\)には入力電圧\(V_{IN}\)が印加されています。この時、インダクタ電流\(i_{L}\)は\(di_{L}\)増加します。ここで、インダクタ電流\(i_{L}\)とインダクタ電圧\(v_{L}\)の有名な関係式\(v_{L}=L\displaystyle\frac{di}{dt}\)を用いると、
\begin{eqnarray}
V_{IN}&=&L\frac{di_{L}}{T_{ON}}\\
{\Leftrightarrow}di_{L}&=&\frac{V_{IN}}{L}{T_{ON}}\tag{1}
\end{eqnarray}
となります。
ここで、スイッチのオン期間\(T_{ON}\)はオンデューティ比\(D\)、周期\(T\)、スイッチング周波数\(f_{SW}\)から以下の式で表されます。
\begin{eqnarray}
T_{ON}=DT=\frac{D}{f_{SW}}\tag{2}
\end{eqnarray}
また、オンデューティ比\(D\)は入力電圧\(V_{IN}\)、出力電圧\(V_{OUT}\)から以下の式で表されます。
\begin{eqnarray}
D=\frac{V_{OUT}-V_{IN}}{V_{OUT}}\tag{3}
\end{eqnarray}
(2)式と(3)式を用いると、(1)式は以下の式となります。
\begin{eqnarray}
di_{L}&=&\frac{V_{IN}}{L}{T_{ON}}\\
&=&\frac{V_{IN}}{L}DT\\
&=&\frac{V_{IN}}{L}×\frac{V_{OUT}-V_{IN}}{V_{OUT}}×\frac{1}{f_{SW}}\tag{4}
\end{eqnarray}
一方、境界条件においては、インダクタ電流\(i_{L}\)の平均値の2倍がインダクタ電流\(i_{L}\)のリプル\(di_{L}\)となります。また、インダクタ電流\(i_{L}\)の平均値は入力電流\(I_{IN}\)と等しいため、以下の式が成り立ちます。
\begin{eqnarray}
di_{L}=2I_{IN}\tag{5}
\end{eqnarray}
(4)式と(5)式より、以下の式が成り立ちます。
I_{IN}=\frac{( V_{OUT}-V_{IN})×V_{IN}}{2×V_{OUT}×f_{SW}×L}\tag{6}
\end{eqnarray}
ここで、入力電力\(P_{IN}\)、出力電力\(P_{OUT}\)、出力電圧\(V_{OUT}\)、効率\({\eta}\)の関係式は以下の式となります。
\begin{eqnarray}
{\eta}=\frac{P_{OUT}}{P_{IN}}=\frac{V_{OUT}I_{OUT}}{V_{IN}I_{IN}}\\
{\Leftrightarrow}I_{IN}=\frac{V_{OUT}I_{OUT}}{V_{IN}×{\eta}}\tag{7}
\end{eqnarray}
(7)式を(6)式に代入すると、境界条件になる出力電流\(I_{OUT}\)を導出することができます。
I_{OUT}=\frac{(V_{OUT}-V_{IN})×{V_{IN}}^2×{\eta}}{2×{V_{OUT}}^2×f_{SW}×L}\tag{8}
\end{eqnarray}
境界条件をシミュレーションで検証する
ここで、連続モードと不連続モードの境界条件をシミュレーションで検証してみます。
入出力条件と各素子値を以下の値とします。
- インダクタンス\(L\)=20uH
- スイッチング周波数\(f_{SW}\)=300kHz
- 入力電圧\(V_{IN}\)=10V
- 出力電圧\(V_{OUT}\)=15V
- 効率\({\eta}\)=100%
上の条件を(8)式に代入すると、出力電流\(I_{OUT}\)は0.185185・・・Aとなります。
シミュレーションで確認すると、出力電流\(I_{OUT}\)が0.185185・・・Aとなるときに臨界モードで動作していることが確認できます。また、その電流値より大きくする(シミュレーションでは0.3A)と連続モードに、小さくする(シミュレーションでは0.05A)と不連続モードで動作していることも確認できます。






