電池の「内部抵抗」と「起電力と端子電圧の関係」について

この記事では『電池の内部抵抗』について

電池の内部抵抗\(r\)とは
電池の起電力\(E\)と端子電圧\(V\)の関係

などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。

電池の内部抵抗とは

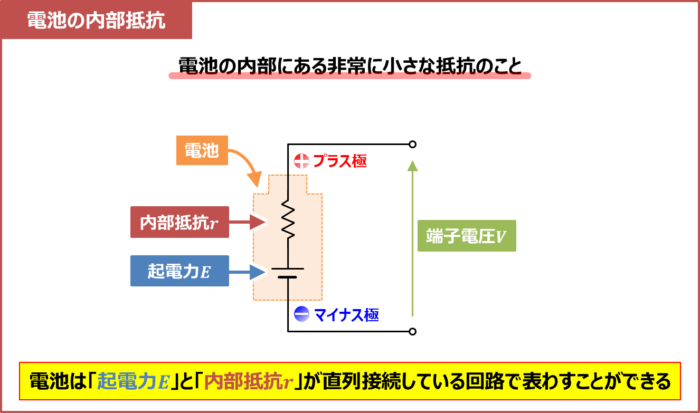
電池の内部には、非常に小さな抵抗\(r\)があります。この抵抗\(r\)を内部抵抗といいます。

そのため、電池は上図に示しているように、「電池の起電力\(E\)」と「内部抵抗\(r\)」が直列接続している回路で表わすことができます。

なお、電池の両端電圧(プラス極とマイナス極の間の電圧)を「端子電圧\(V\)」といいます。

電池の起電力\(E\)と端子電圧\(V\)の関係

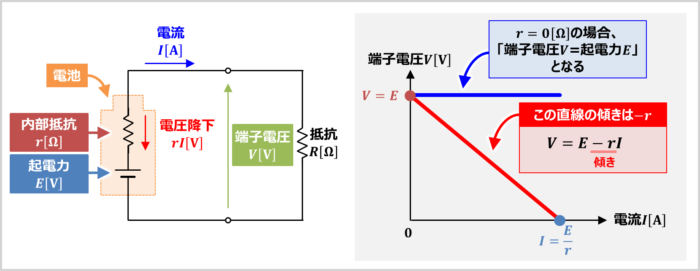
上図に示しているのは、縦軸が「電池の端子電圧\(V\)」、横軸が「電池から流れる電流\(I\)」のグラフです。

電池の内部抵抗\(r\)が\(0{\mathrm{[{\Omega}]}}\)の場合は、電流\(I\)が流れても、内部抵抗\(r\)による電圧降下\(rI\)が生じないため、起電力\(E\)と端子電圧\(V\)が等しくなります(上図の青色の直線)。

しかし、実際の電池は内部抵抗\(r\)を持っているため、電流\(I\)が流れると、内部抵抗\(r\)による電圧降下\(rI\)が生じ、電池の端子電圧\(V\)は起電力\(E\)よりも小さくなります(\(V{≥}E\))。

上図に、起電力が\(E{\mathrm{[V]}}\)で内部抵抗が\(r{\mathrm{[{\Omega}]}}\)の電池に、抵抗\(R{\mathrm{[{\Omega}]}}\)を接続した回路を示しています。この回路において、電池から流れる電流を\(I{\mathrm{[A]}}\)、電池の端子電圧を\(V{\mathrm{[V]}}\)とすると、次式が成り立ちます。

\begin{eqnarray}
E&=&rI+V\\
\\
{\Leftrightarrow}V&=&E-rI\tag{1}
\end{eqnarray}

(1)式から分かるように、「端子電圧\(V\)」は「起電力\(E\)」から「内部抵抗\(r\)による電圧降下\(rI\)」を引いた値になっていることが分かります。また、(1)式より「電池の端子電圧\(V\)」と「電池から流れる電流\(I\)」の関係を表したグラフ(上図の赤色の直線)を描くことができます。

電池から流れる電流\(I\)が増えると、内部抵抗\(r\)による電圧降下\(rI\)が増えるため、端子電圧\(V\)が減少します。

電流\(I\)が\(0{\mathrm{[A]}}\)の時は端子電圧\(V\)と起電力\(E\)が等しくなり(\(V=E\))、電流\(I\)が\(\displaystyle\frac{E}{r}{\mathrm{[A]}}\)の時は端子電圧\(V\)が\(0{\mathrm{[V]}}\)になります。また、グラフの直線の傾きは、(1)式より「\(-r\)」となります。

次に、このグラフの描き方について詳しく説明します。

電池から流れる電流\(I\)が\(0{\mathrm{[A]}}\)の時

(1)式に\(I=0{\mathrm{[A]}}\)を代入すると、「グラフの縦軸(端子電圧\(V\))」と「赤色の直線」の交点を求めることができます。

では実際に計算してみましょう。

(1)式に\(I=0{\mathrm{[A]}}\)を代入すると、端子電圧\(V\)は次式のようになります。

\begin{eqnarray}
V&=&E-rI\\
\\
&=&E-r×0\\
\\
&=&E{\mathrm{[V]}}\tag{2}
\end{eqnarray}

そのため、「グラフの縦軸(端子電圧\(V\))」と「赤色の直線」の交点は\(E{\mathrm{[V]}}\)となります。

電池から流れる電流\(I\)が\(0{\mathrm{[A]}}\)の時は、内部抵抗\(r\)による電圧降下\(rI\)が\(0{\mathrm{[V]}}\)となるため、端子電圧\(V\)と起電力\(E\)が等しくなるのです。

電池から流れる電流が0[A]になる時はどんな時？

抵抗\(R\)を開放状態にした時(電池に抵抗\(R\)を接続していない時)は電流が流れないため、電池から流れる電流\(I\)が\(0{\mathrm{[A]}}\)となります。

端子電圧\(V\)が\(0{\mathrm{[V]}}\)の時

(1)式に\(V=0{\mathrm{[V]}}\)を代入すると、「グラフの横軸(電流\(I\))」と「赤色の直線」の交点を求めることができます。

では実際に計算してみましょう。

(1)式に\(V=0{\mathrm{[V]}}\)を代入すると、電池から流れる電流\(I\)は次式のようになります。

\begin{eqnarray}
V&=&E-rI\\
\\
{\Leftrightarrow}I&=&\frac{E-V}{r}\\
\\
&=&\frac{E-0}{r}\\
\\
&=&\frac{E}{r}\tag{3}
\end{eqnarray}

そのため、「グラフの横軸(電流\(I\))」と「赤色の直線」の交点は\(\displaystyle\frac{E}{r}{\mathrm{[A]}}\)となります。

「電池から流れる電流\(I\)が\(0{\mathrm{[A]}}\)の時(\(V=E{\mathrm{[V]}}の時\))」と「端子電圧\(V\)が\(0{\mathrm{[V]}}\)になる時(\(I=\displaystyle\frac{E}{r}{\mathrm{[A]}}の時\))」を結んだ直線が「電池の端子電圧\(V\)」と「電池から流れる電流\(I\)」の関係を表したグラフ(赤色の直線)となります。

端子電圧\(V\)が0[V]になる時はどんな時？

抵抗\(R\)を短絡状態にした時(抵抗\(R\)が\(0{\mathrm{[{\Omega}]}}\)の時)に端子電圧\(V\)が\(0{\mathrm{[V]}}\)になります。

抵抗\(R\)に電流\(I\)が流れている時、抵抗\(R\)にかかる電圧\(V\)(端子電圧\(V\))は次式となります。

\begin{eqnarray}
V=RI\tag{4}
\end{eqnarray}

(4)式において、抵抗\(R\)を短絡状態にした時は\(R=0{\mathrm{[{\Omega}]}}\)と見なすことができるため、次式に示すように、抵抗\(R\)にかかる電圧(端子電圧\(V\))は\(0{\mathrm{[V]}}\)になります。

\begin{eqnarray}
V=RI=0×I=0{\mathrm{[V]}}\tag{5}
\end{eqnarray}