【アドミタンスとは】『単位』や『計算方法』などのまとめ！

インピーダンスZは「電流の流れにくさ」を表すのに対して、アドミタンスYは「電流の流れやすさ」を表すものです。この記事ではこのアドミタンスYについて

などを図を用いて分かりやすく説明しています。

アドミタンスとは

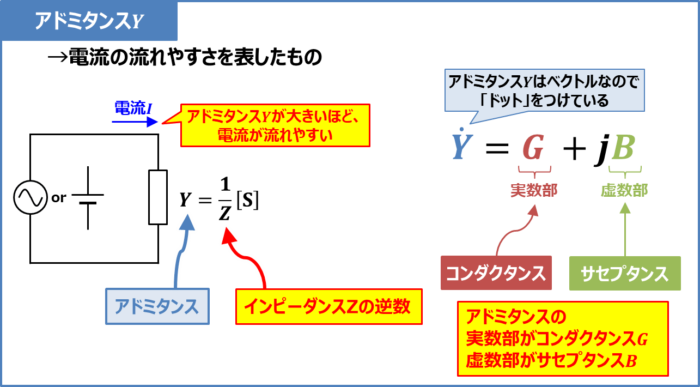
最初にアドミタンスの要点を以下にまとめます。

各要点について順番に説明します。

アドミタンスはインピーダンスZの逆数であり、記号はY、単位は[S]である

アドミタンスは「電流の流れやすさ」を表し、インピーダンスZの逆数となります。記号はY、単位は[S](ジーメンス)となります。式で表すと次式となります。

\begin{eqnarray}
Y=\frac{1}{Z}{\mathrm{[S]}}\tag{1}
\end{eqnarray}

ここで、インピーダンスZは電圧V[V]と電流I[A]の比であるため、次式で表されます。

\begin{eqnarray}
Z=\frac{V}{I}{\mathrm{[{\Omega}]}}\tag{2}
\end{eqnarray}

そのため、(2)式を(1)式に代入すると、アドミタンスY[S]を電圧V[V]と電流I[A]で表すことができ、次式となります。

\begin{eqnarray}
Y=\frac{1}{Z}=\frac{I}{V}{\mathrm{[S]}}\tag{3}
\end{eqnarray}

そのため、アドミタンスY[S]と電圧V[V]が分かれば電流I[A]を求めることができ、アドミタンスY[S]と電流I[A]が分かれば電圧V[V]を求めることができます。

アドミタンスYは大きいほど、電流が流れやすくなる

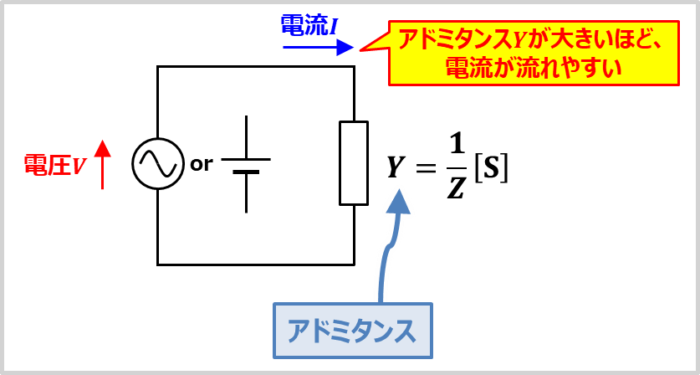
アドミタンスYはインピーダンスZの逆数です。

インピーダンスZは電流の流れにくさを表しています。そのため、インピーダンスZの大きさにより電流Iは以下のように変わります。

一方、アドミタンスYはインピーダンスZの逆数なので、電流の流れやすさを表しています。そのため、アドミタンスYの大きさにより電流Iは以下のように変わります。

また、(4)式ではアドミタンスY[S]と電圧V[V]が分かっている時、流れる電流I[A]は「\(I=YV{\mathrm{[A]}}\)」であることを説明しました。(4)式よりアドミタンスYが大きくなると、電流Iが大きくなることが分かりますね。

アドミタンスの実数部がコンダクタンスG、虚数部がサセプタンスBである

アドミタンスはコンダクタンスGとサセプタンスBを用いると次式で表されます。

\begin{eqnarray}
{\dot{Y}}=G+jB\tag{6}
\end{eqnarray}

コンダクタンスは『ゼロ』または『正の値』となります。抵抗が接続されていない場合はゼロとなり、抵抗が接続されている場合は抵抗の逆数(正の値)となります。

一方、サセプタンスBは『ゼロ』または『正の値』または『負の値』となります。回路にコンデンサやコイルが接続されていない場合はゼロとなります。また、回路が容量性の場合(コンデンサが接続されている回路)は正の値となり、回路が誘導性の場合(コイルが接続されている回路)は負の値となります。

コンダクタンスZは抵抗Rの逆数、サセプタンスBはリアクタンスXの逆数となります。また、インピーダンスZは次式で表されます。

\begin{eqnarray}
{\dot{Z}}=R+jX\tag{7}
\end{eqnarray}

そのため、(1)式と(6)式と(7)式を用いると次式となります。

\begin{eqnarray}
{\dot{Y}}=\frac{1}{{\dot{Z}}}=G+jB+\frac{1}{R+jX}\tag{8}
\end{eqnarray}

分母を有利化すると、次式に変形することができます。

\begin{eqnarray}
{\dot{Y}}=G+jB&=&\frac{1}{R+jX}\\
&=&\frac{R-jX}{(R+jX)(R-jX)}\\
&=&\frac{R-jX}{R^2+X^2}\\
&=&\frac{R}{R^2+X^2}-j\frac{X}{R^2+X^2}\tag{9}
\end{eqnarray}

このように変形することで、アドミタンスYを抵抗RとリアクタンスXの式で表すことができます。

アドミタンスYとインピーダンスZの関係

アドミタンスYとインピーダンスZの関係をまとめると上表のようになります。このように表にすることで全体を整理することができます。

アドミタンスを用いる理由

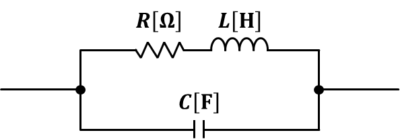
アドミタンスYを用いるのは「並列回路の計算が簡単になるから」です。一例として、上図の抵抗R、コイルL、コンデンサCで構成された回路のインピーダンスZを求めてみましょう。

以下の3つの方法でインピーダンスZを求めます。各々の計算方法を見ると、アドミタンスを用いる方法が一番簡単なのが分かります。

【計算例①】インピーダンスを直接求める方法

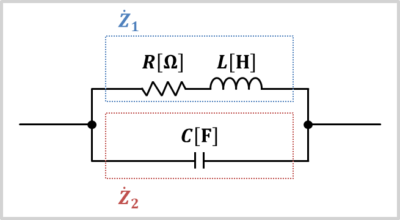
RL直列回路部の直列インピーダンスZ₁とC回路部のインピーダンスZ₂は次式となります。

\begin{eqnarray}
{\dot{Z}}_1&=&R+j{\omega}L\\
{\dot{Z}}_2&=&-j\frac{1}{{\omega}C}\\
\end{eqnarray}

そのため、合成インピーダンスZは次式となります。

\begin{eqnarray}
{\dot{Z}}&=&\frac{1}{\displaystyle\frac{1}{{\dot{Z}}_1}+\displaystyle\frac{1}{{\dot{Z}}_2}}\\
&=&\frac{{\dot{Z}}_1{\dot{Z}}_2}{{\dot{Z}}_1+{\dot{Z}}_2}\\
&=&\frac{\left(R+j{\omega}L\right)\left(-j\displaystyle\frac{1}{{\omega}C}\right)}{\left(R+j{\omega}L\right)+\left(-j\displaystyle\frac{1}{{\omega}C}\right)}\\
&=&\frac{\displaystyle\frac{L}{C}-j\displaystyle\frac{R}{{\omega}C}}{R+j\left({\omega}L-\displaystyle\frac{1}{{\omega}C}\right)}
\end{eqnarray}

式を見やすくするために変形をする必要があります。分母と分子にjωCをかけると次式となります。

\begin{eqnarray}
{\dot{Z}}&=&\frac{R+j{\omega}L}{1-{\omega}^2LC+j{\omega}CR}
\end{eqnarray}

このようにして合成インピーダンスZを求めますが、分母と分子に分数が含まれるため、計算が少し複雑になります。

【計算例②】インピーダンスを直接求める方法(コンデンサのインピーダンスを工夫する)

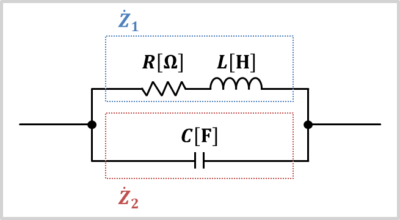
RL直列回路部の直列インピーダンスZ₁とC回路部のインピーダンスZ₂は次式となります。

\begin{eqnarray}
{\dot{Z}}_1&=&R+j{\omega}L\\
{\dot{Z}}_2&=&\frac{1}{j{\omega}C}\\
\end{eqnarray}

「計算例①」と比較すると、コンデンサのインピーダンスZ₂を「\(-j\displaystyle\frac{1}{{\omega}C}\)」→「\(\displaystyle\frac{1}{j{\omega}C}\)」に変更しています。合成インピーダンスZは次式となります。

\begin{eqnarray}
{\dot{Z}}&=&\frac{1}{\displaystyle\frac{1}{{\dot{Z}}_1}+\displaystyle\frac{1}{{\dot{Z}}_2}}\\
&=&\frac{{\dot{Z}}_1{\dot{Z}}_2}{{\dot{Z}}_1+{\dot{Z}}_2}\\
&=&\frac{\left(R+j{\omega}L\right)\left(\displaystyle\frac{1}{j{\omega}C}\right)}{\left(R+j{\omega}L\right)+\left(\displaystyle\frac{1}{j{\omega}C}\right)}\\
&=&\frac{\displaystyle\frac{R+j{\omega}L}{j{\omega}C}}{\displaystyle\frac{1-{\omega}^2LC+j{\omega}CR}{j{\omega}C}}\\
&=&\frac{R+j{\omega}L}{1-{\omega}^2LC+j{\omega}CR}
\end{eqnarray}

インピーダンスを変更することで、「計算例①」よりも計算が少し簡単になったことが分かります。

【計算例③】アドミタンスからインピーダンスを求める方法

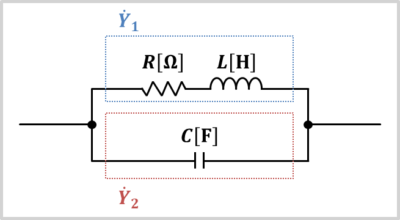
RL直列回路部の直列アドミタンスY₁とC回路部のアドミタンスY₂は次式となります。

\begin{eqnarray}
{\dot{Y}}_1&=&\frac{1}{{\dot{Z}}_1}=\frac{1}{R+j{\omega}L}\\
{\dot{Y}}_2&=&\frac{1}{{\dot{Z}}_2}=\frac{1}{\displaystyle\frac{1}{j{\omega}C}}=j{\omega}C\\
\end{eqnarray}

そのため、合成アドミタンスYは次式となります。

\begin{eqnarray}
{\dot{Y}}=\frac{1}{R+j{\omega}L}+j{\omega}C=\frac{1-{\omega}^2LC+j{\omega}CR}{R+j{\omega}L}
\end{eqnarray}

インピーダンスZはアドミタンスYの逆数なので次式となります。
\begin{eqnarray}
{\dot{Z}}=\frac{1}{{\dot{Y}}}=\frac{R+j{\omega}L}{1-{\omega}^2LC+j{\omega}CR}
\end{eqnarray}

このようにアドミタンスを用いることで、分数の出てくる回数が減り、計算がかなり簡単になります。

アドミタンスの例題

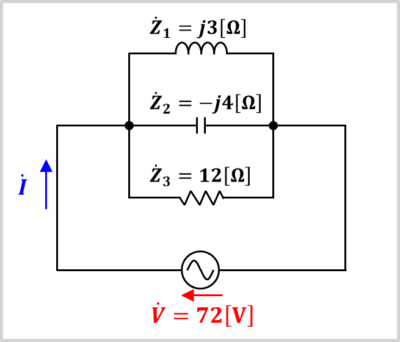
では最後にアドミタンスを用いて、上図の回路に流れる電流の大きさを求めてみましょう。

「インピーダンスから電流を求める方法」と「アドミタンスから電流を求める方法」で別々に解いていきます。

インピーダンスから電流を求める方法

各々のインピーダンスZ₁,Z₂,Z₃は次式で表されます。

\begin{eqnarray}
{\dot{Z}}_1&=&j3{\mathrm{[{\Omega}]}}\\
{\dot{Z}}_2&=&-j4{\mathrm{[{\Omega}]}}\\
{\dot{Z}}_3&=&12{\mathrm{[{\Omega}]}}
\end{eqnarray}

そのため合成インピーダンスZは次式となります。

\begin{eqnarray}
{\dot{Z}}&=&\frac{1}{\displaystyle\frac{1}{{\dot{Z}}_1}+\displaystyle\frac{1}{{\dot{Z}}_2}+\displaystyle\frac{1}{{\dot{Z}}_3}}\\
&=&\frac{1}{\displaystyle\frac{1}{j3}+\displaystyle\frac{1}{-j4}+\displaystyle\frac{1}{12}}\\
&=&\frac{12j}{4-3+j}\\
&=&\frac{12j}{1+j}\\
&=&\frac{12j(1-j)}{(1+j)(1-j)}\\
&=&6j(1-j)\\
&=&6+6j
\end{eqnarray}

回路に流れる電流\({\dot{I}}\)は次式となります。

\begin{eqnarray}
{\dot{I}}=\frac{{\dot{E}}}{{\dot{Z}}}=\frac{72}{6+6j}=\frac{72(6-6j)}{(6+6j)(6-6j)}=6-6j
\end{eqnarray}

したがって、電流の大きさ\(|{\dot{I}}|(=I)\)は次式となります。

\begin{eqnarray}
|{\dot{I}}|=\sqrt{6^2+(-6)^2}=6\sqrt{2}
\end{eqnarray}

アドミタンスから電流を求める方法

各々のアドミタンスY₁,Y₂,Y₃は次式で表されます。

\begin{eqnarray}
{\dot{Y}}_1&=&\frac{1}{{\dot{Z}}_1}=\frac{1}{j3}{\mathrm{[S]}}\\
{\dot{Y}}_2&=&\frac{1}{{\dot{Z}}_2}=\frac{1}{-j4}{\mathrm{[S]}}\\
{\dot{Y}}_3&=&\frac{1}{{\dot{Z}}_3}=\frac{1}{12}{\mathrm{[S]}}
\end{eqnarray}

そのため合成アドミタンスYは次式となります。

\begin{eqnarray}
{\dot{Y}}&=&{\dot{Y}}_2+{\dot{Y}}_1+{\dot{Y}}_3\\
&=&\frac{1}{j3}+\frac{1}{-j4}+\frac{1}{12}\\
&=&\frac{-j4+j3+1}{12}\\
&=&\frac{1-j}{12}
\end{eqnarray}

回路に流れる電流\({\dot{I}}\)は次式となります。

\begin{eqnarray}
{\dot{I}}={\dot{E}}{\dot{Z}}=72×\frac{1-j}{12}=6-6j
\end{eqnarray}

したがって、電流の大きさ\(|{\dot{I}}|(=I)\)は次式となります。

\begin{eqnarray}
|{\dot{I}}|=\sqrt{6^2+(-6)^2}=6\sqrt{2}
\end{eqnarray}

まとめ

この記事では『アドミタンス』について、以下の内容を説明しました。

お読み頂きありがとうございました。

当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。

全記事一覧