この記事では、電気抵抗Rと抵抗率ρの式の導出方法について説明します。
『電気抵抗R』と『抵抗率ρ』の式
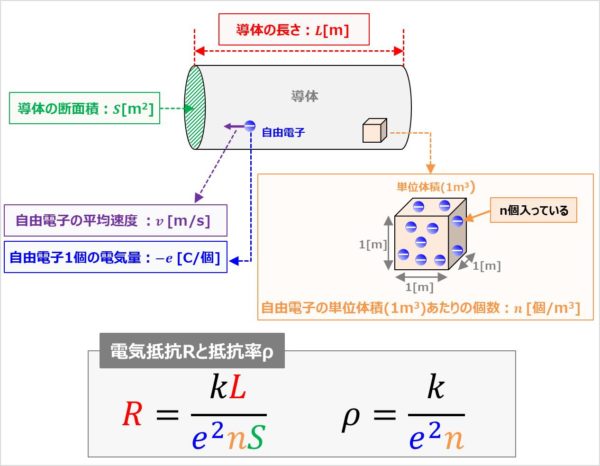
電気抵抗は記号でR、抵抗率は記号でρ(ロー)と表されます。
この電気抵抗Rと抵抗率ρは、自由電子の単位体積(1m3)あたりの個数(数密度と呼ばれる)をn[個/m3]、自由電子の平均速度をv[m/s]、導体の断面積をS[m2]、導体の長さをL[m]とすると、次式で表されます。
R&=&\frac{kL}{e^2nS}\\
{\rho}&=&\frac{k}{e^2n}
\end{eqnarray}
上式のkは比例定数となっています。また、上式のeは『負電荷の自由電子1個の電気量の絶対値または正電荷の陽子1個の電気量』であり、電子素量と呼ばれるものです。
- 負電荷の自由電子1個が持つ電気量:-e=-1.6×10-19[C/個]
- 正電荷の陽子1個が持つ電気量:e=1.6×10-19[C/個]
となります。
では次に、上式の導出方法を詳しく説明していきます。
『電気抵抗R』と『抵抗率ρ』の導出
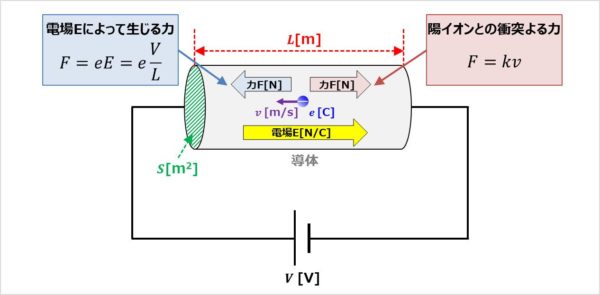
上図に示すように、断面積S[m2]、長さL[m]の導体の両体に電圧V[V]を印加している状況を考えます。
この時、導体内には電場E[N/C]が発生しており、次式で表されます。
\begin{eqnarray}
E=\frac{V}{L}{\mathrm{[N/C]}}\tag{1}
\end{eqnarray}
この電場E[N/C]によって、電気量の大きさがe[C]の自由電子は、力F[N]を左向きに受けます(自由電子はマイナスなので電場Eの方向と逆になります)。電場Eによって生じる力F[N]は次式で表されます。
\begin{eqnarray}
F=eE=e\frac{V}{L}{\mathrm{[N]}}\tag{2}
\end{eqnarray}
上式は有名な『F=qE』の公式において、自由電子の電荷量の大きさがe[C]なので、『q=e』としているだけです。
電場Eによって生じる力F[N]を受けて自由電子は左向きに加速していきます。しかし、自由電子は導体内の陽イオンとの衝突による力(抵抗力)[N]を右向きに受けます。陽イオンとの衝突よる力[N]は自由電子の速度v[m/s]が速いほど大きくなります。すなわち、陽イオンとの衝突よる力[N]は自由電子の速度v[m/s]に比例します。そこで比例定数をkとすると、陽イオンとの衝突よる力[N]は次式で表されます。
\begin{eqnarray}
F=kv{\mathrm{[N]}}\tag{3}
\end{eqnarray}
電場Eによって生じる力F[N]と陽イオンとの衝突よる力[N]が等しくなることで、自由電子の速度v[m/s]は一定となります。この時、自由電子の速度vは次式で表されます。
\begin{eqnarray}
e\frac{V}{L}&=&kv\\
{\Leftrightarrow}v&=&\frac{eV}{kL}{\mathrm{[m/s]}}\tag{4}
\end{eqnarray}
一方、電流の大きさI[A]は自由電子の単位体積(1m3)あたりの個数(数密度と呼ばれる)をn[個/m3]とすると、次式で表されます。
\begin{eqnarray}
I=envS{\mathrm{[A]}}\tag{5}
\end{eqnarray}
上式については以下の記事で詳しく説明してますので、参考にしてください。
-

【電流の大きさ:I=envS】の『導出』と『覚え方』について!
続きを見る
(4)式を(5)式に代入すると、電流の大きさI[A]は次式となります。
\begin{eqnarray}
I=envS=en\left(\frac{eV}{kL}\right)S=\left(\frac{e^2nS}{kL}\right)V{\mathrm{[A]}}\tag{6}
\end{eqnarray}
ここで、オームの法則は次式で表されます。
\begin{eqnarray}
V&=&RI\\
{\Leftrightarrow}I&=&\frac{1}{R}V{\mathrm{[A]}}\tag{7}
\end{eqnarray}
(6)式と(7)式を比較すると、電気抵抗Rは次式で表されます。
R&=&\frac{kL}{e^2nS}\\
&=&\frac{k}{e^2n}\frac{L}{S}{\mathrm{[Ω]}}\tag{8}
\end{eqnarray}
また、電気抵抗Rは抵抗率ρを用いると次式で表されます。
\begin{eqnarray}
R={\rho}\frac{L}{S}\tag{9}
\end{eqnarray}
(8)式と(9)式を比較すると、抵抗率ρは次式で表されます。
{\rho}=\frac{k}{e^2n}{\mathrm{[Ω・m]}}\tag{9}
\end{eqnarray}
これが、電気抵抗Rと抵抗率ρの式の導出方法となっています。なお、抵抗率ρについては以下の記事で詳しく説明してますので、参考にしてください。
-



【抵抗率とは】『単位』や『導電率との違い』などを解説!
続きを見る
まとめ
この記事では電気抵抗Rと抵抗率ρについて、以下の内容を説明しました。
当記事のまとめ
- 電気抵抗Rと抵抗率ρの式
- 電気抵抗Rと抵抗率ρの導出
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。







