この記事ではコモンモードチョークについて基本的な内容を説明した後、働きと等価回路、損失計算などを詳しく説明します。
コモンモードチョークとは
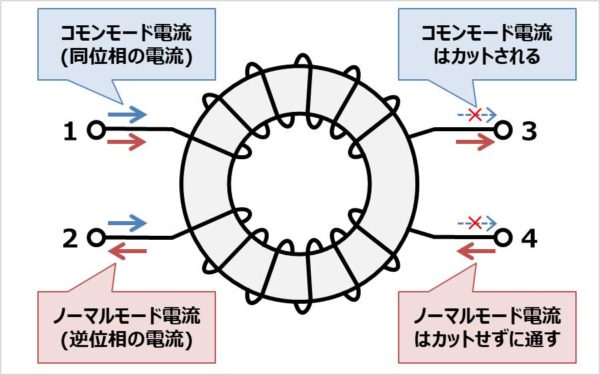
コモンモードチョークとは、コモンモード電流(同位相の電流。上図の青色の電流)をカットし、ノーマルモード電流(逆位相の電流。上図の赤色の電流)はカットせずにそのまま通す素子です。その結果、放射ノイズの発生源であるコモンモードノイズを除去することができます。
コモンモードチョークは1つのコア(高周波用の場合はフェライトのコア)に2本の導線を巻いた構造となっています。そのため、4端子の素子となっています。
コモンモードチョークの働きと等価回路
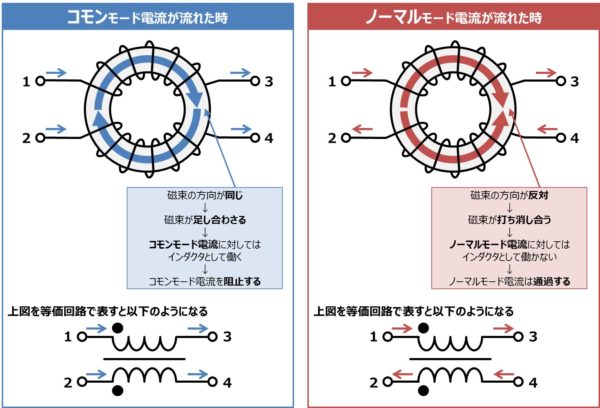
コモンモード電流が流れた時とノーマルモード電流が流れた時におけるコモンモードチョークの働きと等価回路を上図に示します。
- コモンモード電流が流れた時
- ノーマルモード電流が流れた時
各導線に電流が流れることによってコアに発生する磁束の方向が同じになり、磁束が足し合わされます。そのため、コモンモード電流に対してはインダクタとして働くので、コモンモード電流が流れるのを阻止することができます。
各導線に電流が流れることによってコアに発生する磁束の方向が反対になり、磁束が打ち消し合います。そのため、ノーマルモード電流に対してはインダクタとして働かず、ノーマルモード電流は通過します。
ポイント
- コモンモードチョークはチョークコイルに属しており、バラン(バルン)とも呼ばれています。
- コモンモードチョークは構造がトランスと同じであり、同じものを使用できることから、伝送用トランスとも呼ばれています。
- コモンモードチョークは電流定格とインダクタンスで選定を行います。インダクタンスは雑音端子電圧(端雑)の大きさによって決めます。
コモンモードチョークの使用箇所
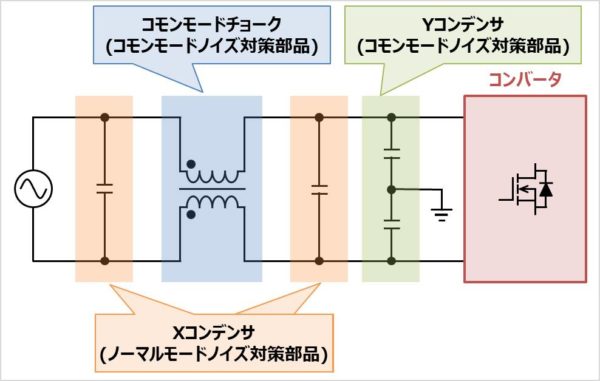
コモンモードチョークは主にスイッチング電源の1次側の交流電流が流れる電源ラインで使われています。この箇所で使用されるコモンモードチョークのことをラインフィルタと呼ぶこともあります。
このコモンモードチョークはスイッチング電源で発生したノイズが電源コードを伝わって出て行くのを防ぐために使用され、Xコンデンサ(アクロス・ザ・ラインコンデンサ)やYコンデンサ(ライン・バイパス・コンデンサ)と共に使用されます。Xコンデンサがノーマルモード(ディファレンシャルモード)のノイズを除去し、Yコンデンサとコモンモードチョークがコモンモードのノイズを除去します。
この電源ラインで使用されるコモンモードチョークには高電圧が印加されます。そのため、電源ライン上で使用する場合には、絶縁性能等の安全規格を満たしているコモンモードチョークコイルを選定する必要があります。定格電圧がAC250Vとなっている製品はほとんどこれらの規定を満たしていますが、使用する場合にはメーカーに別途確認する必要があります。
コモンモードチョークによる損失について
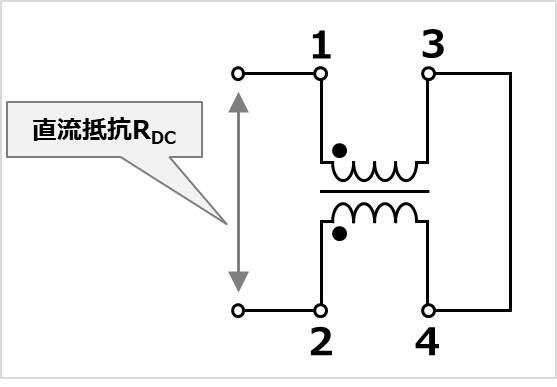
コモンモードチョークの3番端子と4番端子(または1番端子と2番端子)を短絡することで、直流抵抗RDCを測定することができます。
例えば、直流抵抗RDCが0.5Ωで入力電流の実効値IRMSが2Aの場合、コモンモードチョークによる損失PLOSSは以下の値となります。
\begin{eqnarray}
P_{LOSS}=R_{DC}×{I_{RMS}}^2=0.5×2^2=2[W]
\end{eqnarray}
ポイント
- コモンモードチョークには50Hz~60Hzの低周波の交流電流が主に流れます。この程度の周波数の場合、銅損の表皮効果や近接効果による損失や鉄損による損失は無視できるほど小さいので、簡易的に電線の直流抵抗RDCのみで損失を計算することができます。
- 直流抵抗RDCは低抵抗なので4端子法による測定を推奨します。
コモンモードチョークのインダクタンスについて
漏れインダクタンスLE
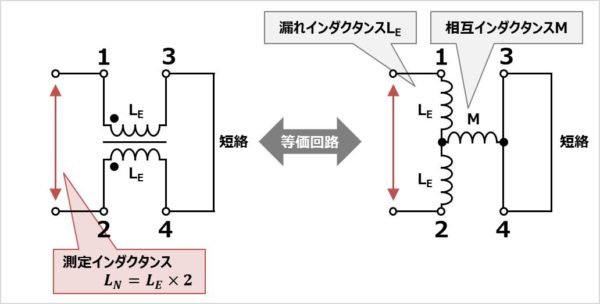
コモンモードチョークの3番端子と4番端子(または1番端子と2番端子)を短絡して測定することでノーマル方向のインダクタンスLNを測定することができます。ノーマル方向のインダクタンスLNは以下の値となります。
\begin{eqnarray}
L_N=L_E×2
\end{eqnarray}
ここで、上式より、漏れインダクタンスLEを計算することができます。
相互インダクタンスM
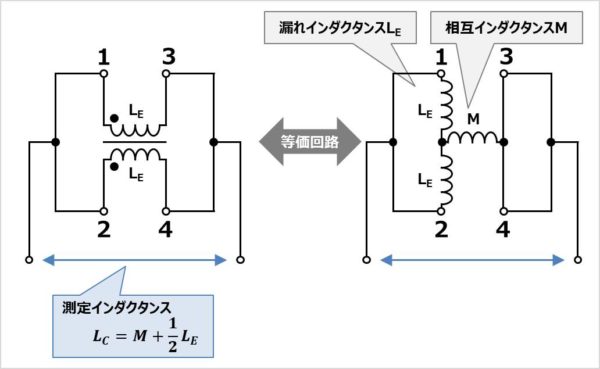
コモンモードチョークの1番端子と2番端子を短絡し、3番端子と4番端子を短絡し、この短絡した両端の端子を測定することで、コモン方向のインダクタンスLCを測定することができます。コモン方向のインダクタンスLCは以下の値となります。
\begin{eqnarray}
L_C=M+\frac{1}{2}L_E
\end{eqnarray}
ここで、上式より、相互インダクタンスMを計算することができます。
ポイント
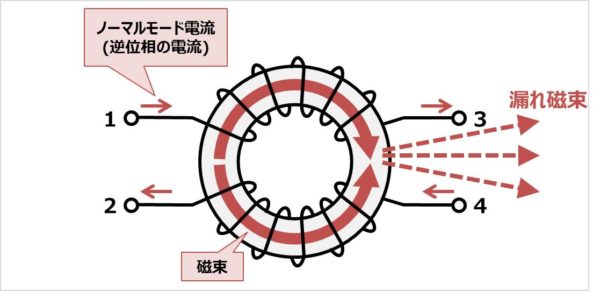
- コモンモードチョークにノーマルモード電流が流れると、下図のような磁束が発生します。2つの巻線から発生した磁束はコアに流れていますが、磁束が打ち消し合う方向なので、2つの巻線の中央付近で磁束が空間に漏れてしまいます。これが漏れインダクタンスLEとして測定されます。

- ノーマルモード電流が原因で外部に漏れ磁束が飛び出します。外部に漏れ磁束が飛び出すということは外部からの磁束がコモンモードチョークに飛び込みやすいということです。コモンモードチョークに飛び込む磁束はノーマル方向の雑音端子電圧に変換されてしまいます。そのため、コモンモードチョークの部品配置は磁束が飛び乗りにくい箇所に配置することをオススメします。
- コモンモードチョークの漏れインダクタンスLEは数~数十μHが一般的です。
- コモンモードチョークの漏れインダクタンスLEが大きいと、コアが飽和しやすくなります。しかし、この漏れインダクタンスLEはノーマル方向の雑音端子電圧を低減させる働きがあります。2モードフィルタなどはこの漏れインダクタンスLEを積極的に利用した部品となっています。すなわち、コアの飽和とノーマル方向の雑音端子電圧対策はトレードオフの関係となっています。
コモンモードチョークの飽和について
コモンモードチョークが飽和すると、コモンモードチョークの働きが低下して、雑音端子電圧(端雑)が増加します。そのため、飽和しないことを確認するために飽和計算を行う必要があります。コモンモード電流はわずかにしか流れていないため、飽和計算する必要はありません。コモンモードチョークにはノーマルモード電流が主に流れているため、ノーマルモード電流によって飽和しないかを計算する必要があります。
まず、磁束密度B[mT]を計算します。磁束密度B[mT]は1つの巻線分の漏れインダクタンスLE[uH]とその巻線に流れる電流のピーク値IPEAKMAX[A]とコアの断面積S[mm2]と片側の巻数N[Turns]から求めることができ、以下の式となります。
\begin{eqnarray}
B[T]=\frac{L_{E}[{\mu}H]×I_{PEAKMAX}[A]}{S[mm^2]×N[Turns]}
\end{eqnarray}
例えば、1つの巻線分の漏れインダクタンスLE[uH]が60uH、その巻線に流れる電流のピーク値IPEAKMAX[A]が6[A]、コアの断面積S[mm2]が25mm^2、片側の巻数N[Turns]が60[Turns]の場合、磁束密度B[mT]は
\begin{eqnarray}
B[T]=\frac{60[{\mu}H]×6[A]}{25[mm^2]×60[Turns]}=240[mT]
\end{eqnarray}
となります。この磁束密度B[mT]に対して、余裕のあるコアを選定する必要があります。
磁束密度Bを下げる方法
コモンモードチョークのキャンセル巻きとバイファイラ巻きについて
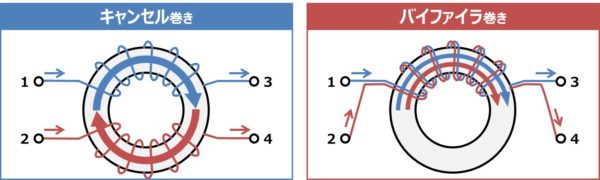
コモンモードチョークにはキャンセル巻きとバイファイラ巻きがあります。キャンセル巻きは2本の導線を別々に巻く巻き方であり、バイファイラ巻きは2本の導線を平行に巻く方法です。キャンセル巻きは分割巻きとも呼ばれています。
まとめ
この記事では『コモンモードチョーク』について、以下の内容を説明しました。
当記事のまとめ
- そもそもコモンモードチョークとは?
- コモンモードチョークの働きと等価回路
- コモンモードチョークの使用箇所
- コモンモードチョークの損失の計算方法
- コモンモードチョークの漏れインダクタンスと相互インダクタンス
- コモンモードチョークの飽和計算
- コモンモードチョークのキャンセル巻きとバイファイラ巻き
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。