この記事では『反転増幅回路』において
- 反転増幅回路の『出力電圧』の導出方法
などを図を用いて分かりやすく説明しています。
反転増幅回路の式
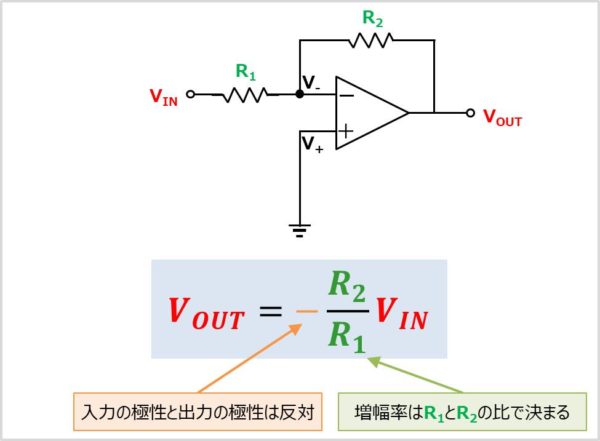
上図に反転増幅回路(Inverting Amplifier Circuit)の式を示します。反転増幅回路の入力電圧を\(V_{IN}\)、出力電圧を\(V_{OUT}\)としたとき、入力電圧\(V_{IN}\)と出力電圧\(V_{OUT}\)の関係式は以下のようになります。
V_{OUT}=-\frac{R_2}{R_1}V_{IN}
\end{eqnarray}
この記事では上式の導出方法について説明します。
なお、反転増幅回路の式を見ると以下のことが分かります。
- 反転増幅回路の増幅率は抵抗\(R_{1}\)と\(R_{2}\)で決まります。ここで注意してほしいのは、入力電圧\(V_{IN}\)に接続されている抵抗\(R_{1}\)が分母にくるということです。間違えて抵抗\(R_{2}\)を分母にしないようにしましょう。
- 入力と出力の極性が反対になります。そのため、反転増幅回路と呼ばれています。
補足
反転増幅回路の式の導出方法
反転増幅回路の式の導出は以下の順序で行うと簡単に求めることができます。この求め方はその他のオペアンプ回路(非反転増幅回路など)にも応用することができます。
導出の順序
- 順序1:入力端子の電圧\(V_{-}\)と\(V_{+}\)が等しい
- 順序2:反転入力端子\(V_{-}\)の電圧を求める
- 順序3:非反転増幅端子\(V_{+}\)の電圧を求める
- 順序4:「順序1」~「順序3」を合体する
順序1:入力端子の電圧\(V_{-}\)と\(V_{+}\)が等しい
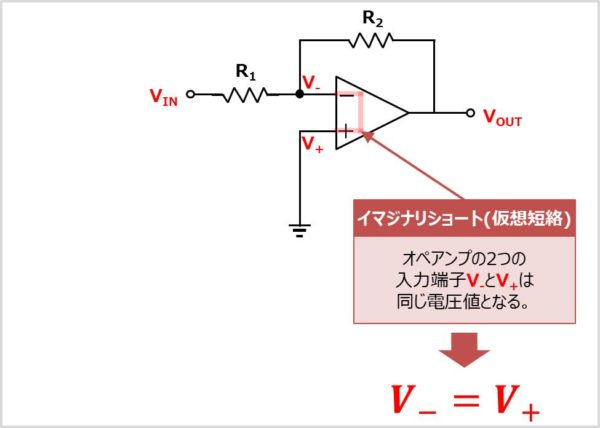
オペアンプの入力端子はイマジナリショート(仮想短絡)のため、反転入力端子\(V_{-}\)と非反転増幅端子\(V_{+}\)の電圧は等しくなります。そのため、以下の式が成り立ちます。
\begin{eqnarray}
V_{-}=V_{+}
\end{eqnarray}
【補足】イマジナリショート(仮想短絡)とは?
順序2:反転入力端子\(V_{-}\)の電圧を求める
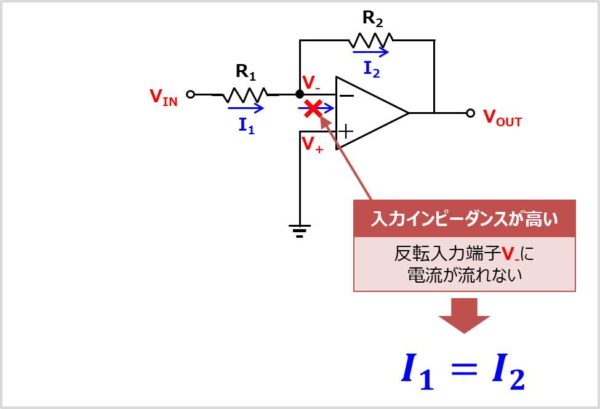
次に反転入力端子\(V_{-}\)の電圧を求めます。オペアンプは入力インピーダンスが高いという特徴があります。そのため、反転入力端子\(V_{-}\)に電流が流れません。
したがって、抵抗\(R_{1}\)に流れる電流\(I_{1}\)と抵抗\(R_{2}\)に流れる電流\(I_{2}\)が等しくなります。そのため、以下の式が成り立ちます。
\begin{eqnarray}
I_{1}&=& I_{2}\\
{\Leftrightarrow}\frac{V_{IN}-V_{-}}{R_1}&=&\frac{V_{-}- V_{OUT}}{R_2}
\end{eqnarray}
上式を変形すると、以下の式となります。
\begin{eqnarray}
V_{-}=\frac{R_1V_{OUT}+R_2 V_{IN}}{R_1+ R_2}
\end{eqnarray}
順序3:非反転増幅端子\(V_{+}\)の電圧を求める
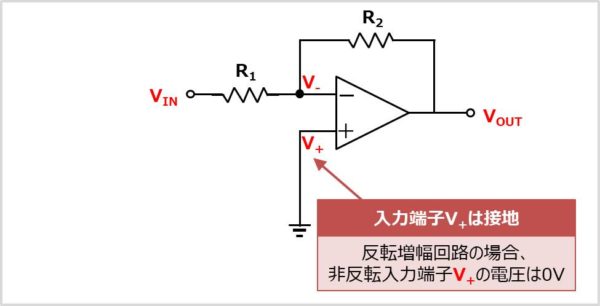
反転増幅回路の場合、非反転増幅端子\(V_{+}\)は接地されているため、0Vとなります。そのため、以下の式が成り立ちます。
\begin{eqnarray}
V_{+}=0
\end{eqnarray}
順序4:「順序1」~「順序3」を合体する
「順序1」~「順序3」で求めた式を用いると、以下の式となり、反転増幅回路の式を求めることができます。
\begin{eqnarray}
V_{-}&=&V_{+}\\
{\Leftrightarrow}\frac{R_1V_{OUT}+R_2 V_{IN}}{R_1+ R_2}&=&0\\
{\Leftrightarrow} V_{OUT}&=&-\frac{R_2}{R_1}V_{IN}
\end{eqnarray}
【補足】反転増幅回路の見分け方
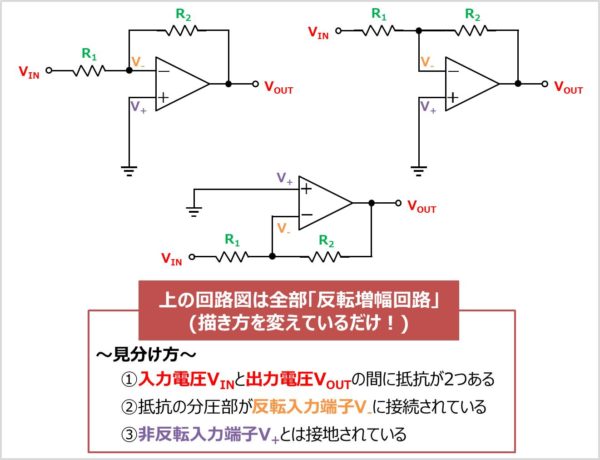
反転増幅回路は参考書やネット等で様々な描き方があります。上図の回路図は全部同じ「反転増幅回路」です。
見分け方は以下のように行います。
- 入力電圧\(V_{IN}\)と出力電圧\(V_{OUT}\)の間に抵抗が2つある
- 抵抗の分圧部が反転入力端子\(V_{-}\)に接続されている
- 非反転入力端子\(V_{+}\)とは接地されている






