『力率』のまとめ！計算方法・単位・遅れ力率・進み力率・無効率について

この記事では『力率』について

力率の『計算方法』と『単位』
『遅れ力率』とは
『進み力率』とは
『無効率』とは

などを図を用いて分かりやすく説明しています。

力率とは？

力率について簡潔に説明すると、

力率は、交流回路で用いられる用語であり、皮相電力\(S\)に対してどれくらい有効電力\(P\)になるかを示す指標となります。また、力率は\({\cos}{\theta}\)で表され、英語では『Power Factor』と書きます。

・・・少し難しいですね。

では、これから力率について出来るだけ分かりやすく説明します。

まず、入力部が交流電源である交流回路の電力(交流電力)には有効電力\(P\)・無効電力\(Q\)・皮相電力\(S\)という3種類の電力があります。

各種類の式をまとめると以下のようになります。

有効電力\(P\)

\begin{eqnarray}
P=VI{\cos}{\theta}=S{\cos}{\theta}[W] \tag{1}
\end{eqnarray}

無効電力\(Q\)・

\begin{eqnarray}
Q=VI{\sin}{\theta}=S{\sin}{\theta}[var] \tag{2}
\end{eqnarray}

皮相電力\(S\)

\begin{eqnarray}
S=VI [VA] \tag{3}
\end{eqnarray}

上記の3式において、有効電力\(P\)・無効電力\(Q\)・皮相電力\(S\)の関係を数式で表すと以下のようになります。

\begin{eqnarray}
皮相電力S^2&=&有効電力P^2+有効電力Q^2\\
{\Leftrightarrow}皮相電力S&=& \sqrt{有効電力P^2+有効電力Q^2}\tag{4}
\end{eqnarray}

上式で出てきた\({\cos}{\theta}\)のことを力率(Power Factor)といいます。

(1)式と(4)式を用いると、力率\({\cos}{\theta}\)は以下の式で表されます。

\begin{eqnarray}
{\cos}{\theta}=\frac{P}{S}=\frac{P}{ \sqrt{ P^2+Q^2}}
\end{eqnarray}

これより、力率\({\cos}{\theta}\)は皮相電力\(S\)が有効電力\(P\)になる割合を表していることが分かります。言い換えると、皮相電力\(S\)のうち有効電力\(P\)として取り出せる割合がどれくらいかを表す指標ということになります。なお、力率\({\cos}{\theta}\)は割合を示す量なので、単位はありません。

また、力率\({\cos}{\theta}\)の最小値は\({\cos}90°=0\)であり、力率の最大値は\({\cos}0°=1\)となります。すなわち力率の範囲は0～1となります。

補足

力率\({\cos}{\theta}\)は100倍して0%～100%で表すこともあります。
力率\({\cos}{\theta}\)は「電圧に対して電流がどれだけ遅れているかor進んでいるか」を数値化した指標にもなります。力率\({\cos}{\theta}\)が1に近づくほど、電圧と電流の位相差が小さいことになります。

なお、有効電力\(P\)・無効電力\(Q\)・皮相電力\(S\)について詳しい内容は以下の記事に記載していますので参考にしてください。

: 有効電力・無効電力・皮相電力の違いを分かりやすく解説します！
続きを見る

遅れ力率と進み力率の違い

力率\({\cos}{\theta}\)には遅れ力率と進み力率があります。

例えば、下図のような交流回路を考えてみます。

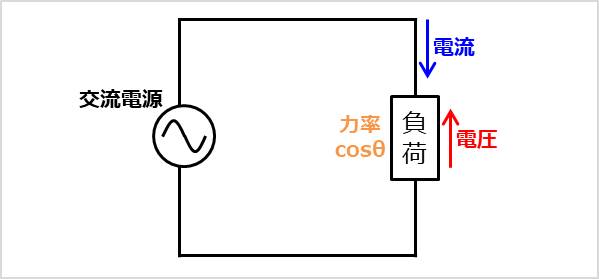
この交流回路において負荷がコイル成分を含むか、コンデンサ成分を含むかによって遅れ力率か進み力率かが決まります。

遅れ力率

負荷がコイル成分を含む場合(誘導性負荷の場合。例えば、抵抗とコイルの直列接続回路など)、電圧に対して電流の位相が遅れます。この時の力率\({\cos}{\theta}\)を遅れ力率といいます。

進み力率

負荷がコンデンサ成分を含む場合(容量性負荷の場合。例えば、抵抗とコンデンサの直列接続回路など)、電圧に対して電流の位相が進みます。この時の力率\({\cos}{\theta}\)を進み力率といいます。

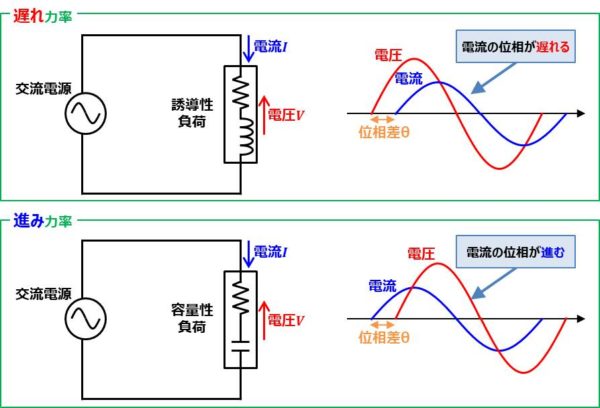
ではこれから遅れ力率と進み力率について図を用いて詳しく説明します。

遅れ力率

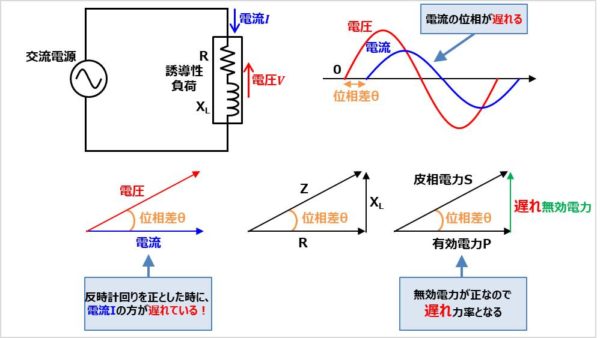
負荷がコイル成分を含む場合、電圧\(V\)に対して電流\(I\)の位相が遅れます。この時の力率\({\cos}{\theta}\)を遅れ力率と言います。

電流\(I\)の位相が遅れる・・・少しイメージが難しいかもしれませんね。

電流\(I\)の方が位相を遅れている表現として参考書などで様々な表現方法がありますので紹介します。

負荷にかかる電圧\(V\)と負荷に流れる電流\(I\)のベクトル図における説明

負荷にかかる電圧\(V\)と負荷に流れる電流\(I\)のベクトル図で書くと、反時計回りを正としたときに、電流\(I\)の方が遅れていると考えると分かりやすいと思います。時間軸(位相軸)で考えると、以下の場合、電圧\(V\)に対して電流\(I\)の位相が遅れていることになります。

負荷にかかる電圧\(V\)と負荷に流れる電流\(I\)の波形における説明

電圧波形は位相が\(0°\)の時に0Vから増加していますが、電流波形は位相が\({\theta}\)の時に0Aから増加しています。そのため、電流\(I\)の方が位相が遅れているということになります。

無効電力\(Q\)の正負における説明

有効電力\(P\)、無効電力\(Q\)、皮相電力\(S\)のベクトル図で考えると、遅れ力率の時には、無効電力\(Q\)が正となります。これは、抵抗\(R\)とコイルの誘導リアクタンス\(X_L\)の関係図より、誘導リアクタンス\(X_L\)はベクトルが正の方向となりますので、無効電力\(Q\)が正となります。

進み力率

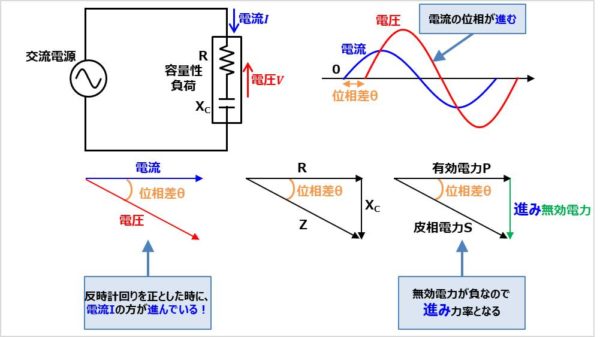
遅れ力率と考え方は同じです。

負荷がコンデンサ成分を含む場合、電圧\(V\)に対して電流\(I\)の位相が進みます。この時の力率\({\cos}{\theta}\)を進み無効電力と言います。

電流\(I\)の位相が進む・・・少しイメージが難しいかもしれませんね。

電流\(I\)の方が位相を進んでいる表現として参考書などで様々な表現方法がありますので紹介します。

負荷にかかる電圧\(V\)と負荷に流れる電流\(I\)のベクトル図における説明

負荷にかかる電圧\(V\)と負荷に流れる電流\(I\)のベクトル図で書くと、反時計回りを正としたときに、電流\(I\)の方が進んでいると考えると分かりやすいと思います。時間軸(位相軸)で考えると、以下の場合、電圧\(V\)に対して電流\(I\)の位相が進んでいることになります。

負荷にかかる電圧\(V\)と負荷に流れる電流\(I\)の波形における説明

電流波形は位相が\(0°\)の時に0Vから増加していますが、電圧波形は位相が\({\theta}\)の時に0Vから増加しています。そのため、電流\(I\)の方が位相が進んでいるということになります。

無効電力\(Q\)の正負における説明

有効電力\(P\)、無効電力\(Q\)、皮相電力\(S\)のベクトル図で考えると、進み力率の時には、無効電力\(Q\)が負となります。これは、抵抗\(R\)とコンデンサの容量リアクタンス\(X_C\)の関係図より、容量リアクタンス\(X_C\)はベクトルが負の方向となりますので、無効電力\(Q\)が負となります。

力率の関連用語

では最後に力率の関連用語である無効率と力率改善について説明します。

無効率とは

力率の関連用語として無効率というものがあります。

以下の有効電力\(P\)の式に出てくる\({\cos}{\theta}\)が力率であることを説明しました。
\begin{eqnarray}
P=VI{\cos}{\theta}=S{\cos}{\theta}[W]
\end{eqnarray}

一方、無効率とは、以下の無効電力\(Q\)の式に出てくる\({\sin}{\theta}\)のことを指します。
\begin{eqnarray}
Q=VI{\sin}{\theta}=S{\sin}{\theta}[var]
\end{eqnarray}

無力率ではなく無効率なので注意してくださいね。

力率改善とは

例えば、皮相電力\(S\)が100[VA]で有効電力\(P\)が70[W]の場合、力率\({\cos}{\theta}\)は
\begin{eqnarray}
{\cos}{\theta}=\frac{70}{100}=0.7
\end{eqnarray}
となります。ここで回路の改善等を行い、有効電力\(P\)を80[W]に上げると、力率\({\cos}{\theta}\)は
\begin{eqnarray}
{\cos}{\theta}=\frac{80}{100}=0.8
\end{eqnarray}
となり、力率\({\cos}{\theta}\)が増加します。このように力率\({\cos}{\theta}\)を増加させることを力率改善と言います。