有効電力・無効電力・皮相電力の違いを分かりやすく解説します！

この記事では『有効電力』・『無効電力』・『皮相電力』について

『有効電力』・『無効電力』・『皮相電力』の違い

などを図を用いて分かりやすく説明しています。

直流電力と交流電力の違い

有効電力・無効電力・皮相電力は交流電力で用いられる用語になります。

そのため、まず直流電力と交流電力の違いから説明をします。

直流電力

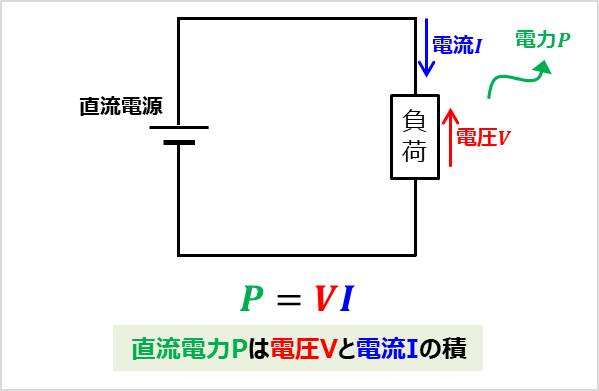
入力部が直流電源である直流回路の電力(直流電力)は電圧と電流の積となります。直流電源の電圧も一定であり、負荷に流れる電流も一定となります。例えば、負荷にかかる電圧を\(V\)、負荷に流れる電流を\(I\)とすると、直流電力\(P\)は以下の式で表されます。
\begin{eqnarray}
P=VI
\end{eqnarray}

交流電力

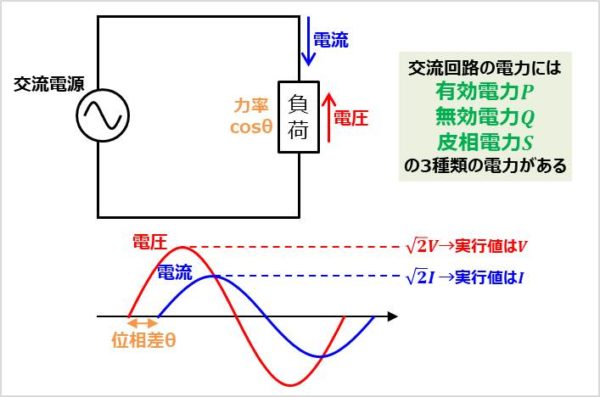
入力部が交流電源である交流回路の電力(交流電力)には有効電力\(P\)・無効電力\(Q\)・皮相電力\(S\)という3種類の電力があります。この記事では、有効電力\(P\)・無効電力\(Q\)・皮相電力\(S\)について説明しますが、その際に以下のパラメータ・用語を用います。

実行値

交流回路における電圧と電流には実行値を使用します。以下の交流回路の場合、交流電圧の実行値は\(V\)、交流電流の実行値は\(I\)となります。

位相差\({\theta}\)

負荷にかかる電圧と負荷に流れる電流の位相差を表す\({\theta}\)を使用します。以下の交流回路の場合、電圧は電流より位相が\({\theta}\)進んでいるということになります。

力率\({\cos}{\theta}\)

負荷が消費する電力の割合を表す力率\({\cos}{\theta}\)を使用します。

では、まず有効電力\(P\)から説明します。

有効電力・無効電力・皮相電力の違い

有効電力

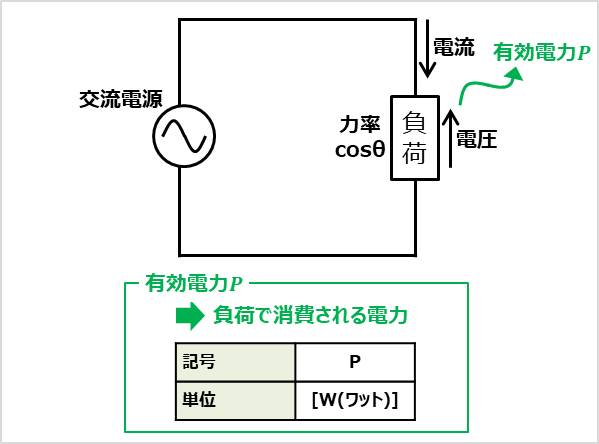
有効電力\(P\)は負荷で消費される電力です(負荷で消費されない電力は無効電力\(Q\)となります。無効電力については後ほど説明します)。有効電力は記号を\(P\)で表します。また、単位は[W(ワット)]となります。

例えば、下図のような交流回路を考えてみます。

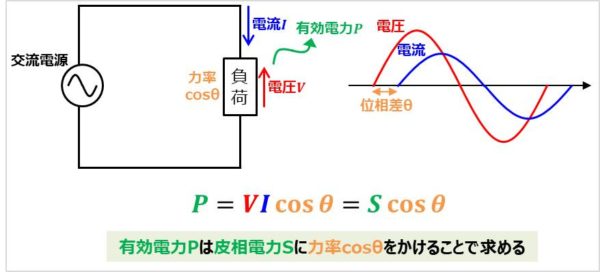
この交流回路において、負荷にかかる電圧の実行値が\(V\)、負荷に流れる電流の実行値が\(I\)、電圧と電流の位相差が\({\theta}\)、力率が\({\cos}{\theta}\)だとすると、有効電力\(P\)は以下の式で表すことができます。

\begin{eqnarray}
P=VI{\cos}{\theta}=S{\cos}{\theta}[W]
\end{eqnarray}

上記の式より、有効電力\(P\)は皮相電力\(S\)に力率\({\cos}{\theta}\)をかけることで求めることができるということが分かります。有効電力\(P\)は負荷が消費する電力なので、負荷は\(P=S{\cos}{\theta}[W]\)の電力を消費し続けていることになります。

なお、この有効電力\(P\)は負荷が消費する電力なので、消費電力と呼ぶこともあります。また、単に「電力」といったらこの有効電力(消費電力)のことを指します。

有効電力の身近な例

電気機器のカタログには有効電力(消費電力)が表記されています。例えば、「ドライヤーの消費電力：1000W」、「扇風機の消費電力：50W」というように表記されている。例えば、1000Wのドライヤーを使うと、1000Wの電力をドライヤーで消費することを表します。

無効電力

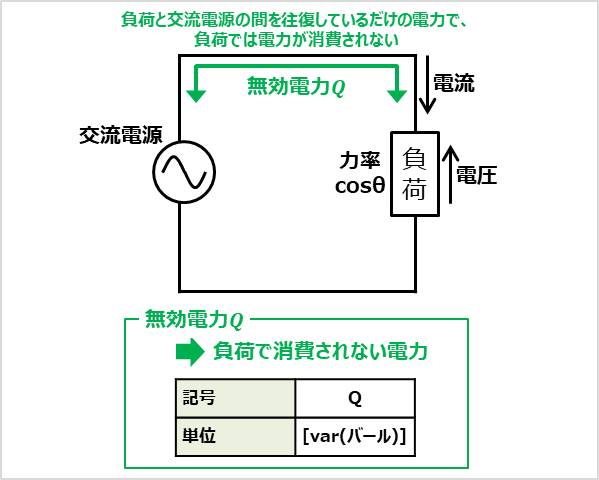
無効電力\(Q\)は負荷で消費されない電力です。無効電力は記号を\(Q\)で表します。また、単位は[var(バール)]となります。

例えば、下図のような交流回路を考えてみます。

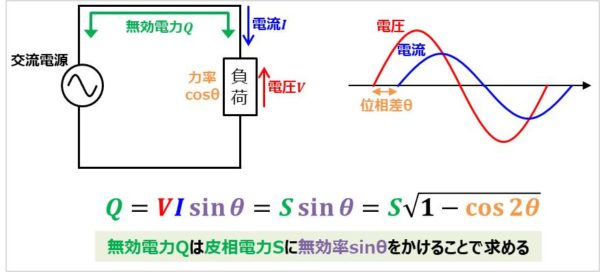
この交流回路において、負荷にかかる電圧の実行値が\(V\)、負荷に流れる電流の実行値が\(I\)、電圧と電流の位相差が\({\theta}\)、力率が\({\cos}{\theta}\)だとすると、無効電力\(Q\)は以下の式で表すことができます。
\begin{eqnarray}
Q=VI{\sin}{\theta}=S{\sin}{\theta}=VI\sqrt{1-{\cos}2{\theta}}[var]
\end{eqnarray}

有効電力\(P\)は皮相電力\(S\)に力率\({\cos}{\theta}\)をかけることで求めることができましたが、上記の式より、無効電力\(Q\)は皮相電力\(S\)に\({\sin}{\theta}\)をかけることで求めることができます。なお、この\({\sin}{\theta}\)のことを無効率といいます。

この無効電力\(Q\)は交流電源から供給される電力のうち、何も仕事をせずに交流電源に戻ってくる電力となります。つまり、負荷と交流電源の間を往復しているだけの電力であり、負荷では電力が消費されません(そのため無効電力\(Q\)と呼ばれています)。

この無効電力\(Q\)は位相差\({\theta}\)が大きいほど、大きくなる(\({\sin}{\theta}\)が大きくなる)ため、位相差\({\theta}\)を発生させる原因となる負荷のコイル成分やコンデンサ成分の大きさによって大きさが変化します。

負荷がコイル成分を含む場合(誘導性負荷の場合。例えば、抵抗とコイルの直列接続回路など)、電圧に対して電流の位相が遅れます。この時の無効電力\(Q\)を遅れ無効電力といいます。一方、負荷がコンデンサ成分を含む場合(容量性負荷の場合。例えば、抵抗とコンデンサの直列接続回路など)、電圧に対して電流の位相が進みます。この時の無効電力\(Q\)を進み無効電力といいます。

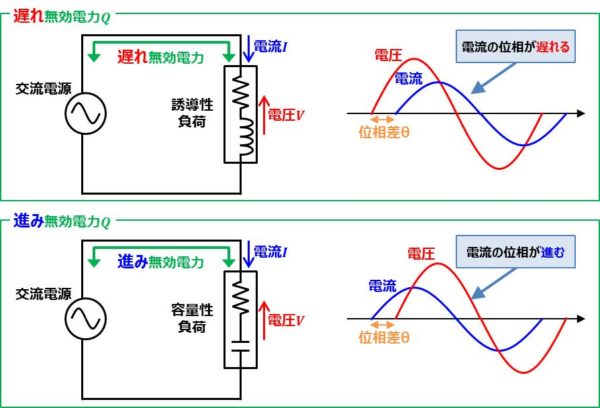
この遅れ無効電力と進み無効電力について詳しく説明すると長くなってしまうので、この記事の後半に記載しています。

皮相電力

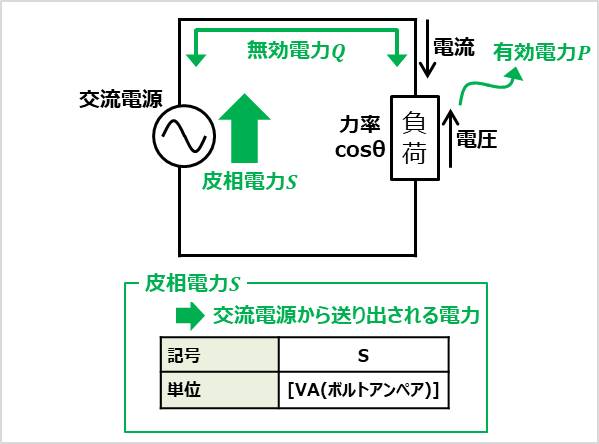
皮相電力\(S\)は交流電源から送り出される電力です。皮相電力は記号を\(S\)で表します。また、単位は[VA(ボルトアンペア)]となります。

例えば、下図のような交流回路を考えてみます。

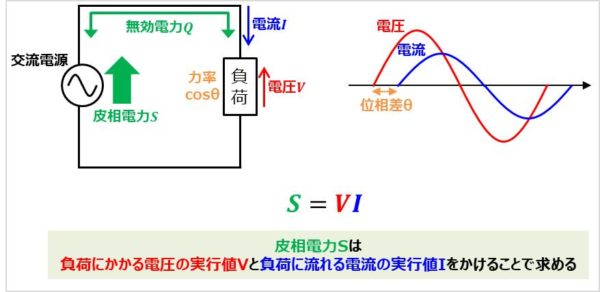
この交流回路において、負荷にかかる電圧の実行値が\(V\)、負荷に流れる電流の実行値が\(I\)だとすると、皮相電力\(S\)は以下の式で表すことができます。
\begin{eqnarray}
S=VI [VA]
\end{eqnarray}
上記の式より、皮相電力\(S\)は負荷にかかる電圧の実行値\(V\)と負荷に流れる電流の実行値\(I\)の積であることが分かります。

今まで、有効電力\(P\) (←負荷で消費される電力)と無効電力\(Q\)(←負荷と交流電源の間を往復しているだけの電力)を学びました。この有効電力\(P\)も無効電力\(Q\)のどちらも交流電源から電力が供給されています(送り出されています)。

そのため、この皮相電力\(S\)は有効電力\(P\)と無効電力\(Q\)を合わせた電力ということになります。

合わせた電力ですが、有効電力\(P\)と無効電力\(Q\)を足し算するわけではありません。有効電力のベクトルと無効電力のベクトルを合成した電力が皮相電力\(S\)となります。このことについては、次項の「有効電力・無効電力・皮相電力の関係」でこのことについて詳しく説明します。

有効電力・無効電力・皮相電力の関係

交流電力には、有効電力\(P\)・無効電力\(Q\)・皮相電力\(S\)の3種類あることを説明しました。各種類の式をまとめると以下のようになります。

有効電力\(P\)

\begin{eqnarray}
P=VI{\cos}{\theta}=S{\cos}{\theta}[W]
\end{eqnarray}

無効電力\(Q\)・

\begin{eqnarray}
Q=VI{\sin}{\theta}=S{\sin}{\theta}[var]
\end{eqnarray}

皮相電力\(S\)

\begin{eqnarray}
S=VI [VA]
\end{eqnarray}

上記の3式において、有効電力\(P\)・無効電力\(Q\)・皮相電力\(S\)の関係を数式で表すと以下のようになります。

\begin{eqnarray}
皮相電力S^2&=&有効電力P^2+有効電力Q^2\\
{\Leftrightarrow}皮相電力S&=& \sqrt{有効電力P^2+有効電力Q^2}
\end{eqnarray}

上式の導出

三角関数の公式\({{\cos}{\theta}}^2+{{\sin}{\theta}}^2=1\)を用います。
\begin{eqnarray}
P^2+Q^2＝S^2({{\cos}{\theta}}^2+{{\sin}{\theta}}^2)=S^2
\end{eqnarray}

また、有効電力\(P\)・無効電力\(Q\)・皮相電力\(S\)の関係を図で表すと以下のようになります。

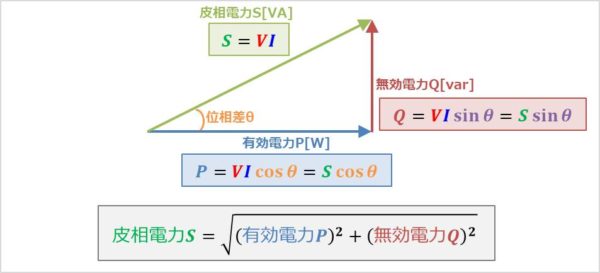
上図より、有効電力\(P\)のベクトルと無効電力\(Q\)のベクトルを合成した電力が皮相電力\(S\)となり、直角三角形となることが分かります。

皮相電力\(S\)は交流電源から送り出される電力なので、上図から分かるように、無効電力\(Q\)が大きくなると、交流電源から送り出す電力が大きくなることが分かります。つまり、無効電力\(Q\)が大きいと、交流電源の負担が大きくなることになります。

補足

一般家庭の電気代は、有効電力によって決まっています。一般家庭に設置されている電力メーター(電力量計)は有効電力を計算しているのです。そのため、無効電力がどれだけ含まれていても、電気料金には関係ないので安心してください。

【補足】遅れ無効電力と進み無効電力について

最後に遅れ無効電力と進み無効電力について説明します。

遅れ無効電力

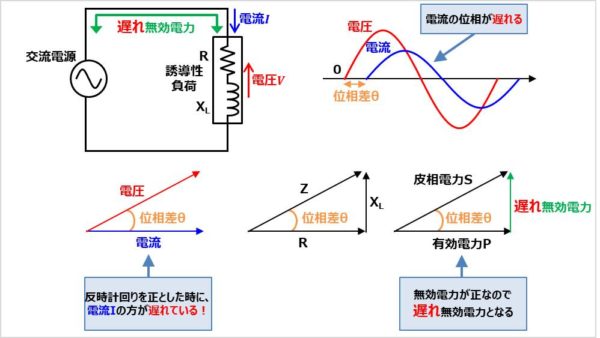
負荷がコイル成分を含む場合、電圧\(V\)に対して電流\(I\)の位相が遅れます。この時の無効電力\(Q\)を遅れ無効電力と言います。

電流\(I\)の位相が遅れる・・・少しイメージが難しいかもしれませんね。

電流\(I\)の方が位相を遅れている表現として参考書などで様々な表現方法がありますので紹介します。

負荷にかかる電圧\(V\)と負荷に流れる電流\(I\)のベクトル図における説明

負荷にかかる電圧\(V\)と負荷に流れる電流\(I\)のベクトル図で書くと、反時計回りを正としたときに、電流\(I\)の方が遅れていると考えると分かりやすいと思います。時間軸(位相軸)で考えると、以下の場合、電圧\(V\)に対して電流\(I\)の位相が遅れていることになります。

負荷にかかる電圧\(V\)と負荷に流れる電流\(I\)の波形における説明

電圧波形は位相が\(0°\)の時に0Vから増加していますが、電流波形は位相が\({\theta}\)の時に0Aから増加しています。そのため、電流\(I\)の方が位相が遅れているということになります。

無効電力\(Q\)の正負における説明

有効電力\(P\)、無効電力\(Q\)、皮相電力\(S\)のベクトル図で考えると、遅れ無効電力の時には、無効電力\(Q\)が正となります。これは、抵抗\(R\)とコイルの誘導リアクタンス\(X_L\)の関係図より、誘導リアクタンス\(X_L\)はベクトルが正の方向となりますので、無効電力\(Q\)が正となります。

進み無効電力

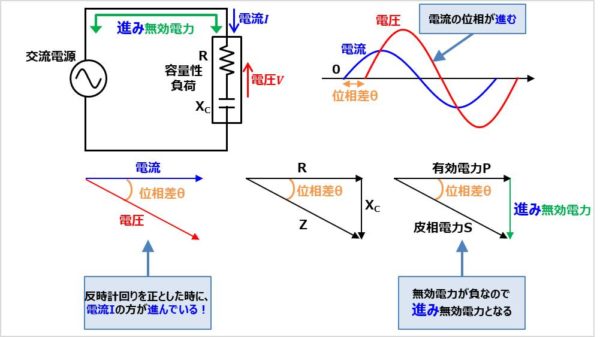
遅れ無効電力と考え方は同じです。

負荷がコンデンサ成分を含む場合、電圧\(V\)に対して電流\(I\)の位相が進みます。この時の無効電力\(Q\)を進み無効電力と言います。

電流\(I\)の位相が進む・・・少しイメージが難しいかもしれませんね。

電流\(I\)の方が位相を進んでいる表現として参考書などで様々な表現方法がありますので紹介します。

負荷にかかる電圧\(V\)と負荷に流れる電流\(I\)のベクトル図における説明

負荷にかかる電圧\(V\)と負荷に流れる電流\(I\)のベクトル図で書くと、反時計回りを正としたときに、電流\(I\)の方が進んでいると考えると分かりやすいと思います。時間軸(位相軸)で考えると、以下の場合、電圧\(V\)に対して電流\(I\)の位相が進んでいることになります。

負荷にかかる電圧\(V\)と負荷に流れる電流\(I\)の波形における説明

電流波形は位相が\(0°\)の時に0Vから増加していますが、電圧波形は位相が\({\theta}\)の時に0Vから増加しています。そのため、電流\(I\)の方が位相が進んでいるということになります。

無効電力\(Q\)の正負における説明

有効電力\(P\)、無効電力\(Q\)、皮相電力\(S\)のベクトル図で考えると、進み無効電力の時には、無効電力\(Q\)が負となります。これは、抵抗\(R\)とコンデンサの容量リアクタンス\(X_C\)の関係図より、容量リアクタンス\(X_C\)はベクトルが負の方向となりますので、無効電力\(Q\)が負となります。