【電源】『ブリッジダイオード』の選定方法！式計算について

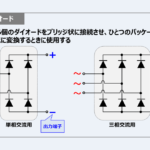
交流入力電圧を直流電圧に変換する際に用いるブリッジダイオードの選定方法について説明します。

ブリッジダイオードの選定方法

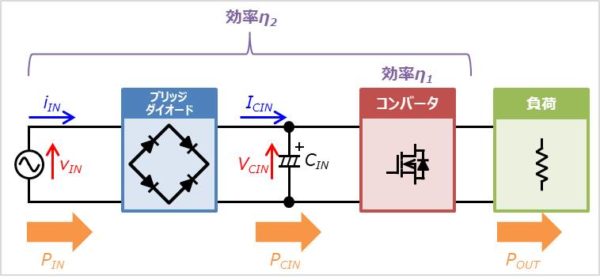
ブリッジダイオードは定格電圧、定格電流、サージ電流、消費電力、温度上昇を計算することにより選定を行うことができます。この記事では、以下に示した電源の条件において、ブリッジダイオードをどのように選定するかを式を用いて説明します。

定格電圧

ブリッジダイオードの必要定格電圧\(V_{RATED}\)は『入力AC電圧の最大値\(V_{INRMS (MAX)}\)のピーク値\(V_{INPEAK(MAX)}\)』にディレーティングを考慮して決定します。

上記の条件の場合、入力AC電圧の最大値のピーク値\(V_{INPEAK(MAX)}\)は以下の値となります。
\begin{eqnarray}
V_{INPEAK(MAX)}&=&V_{INRMS(MAX)}×\sqrt{2}\\
&=&264×\sqrt{2}\\
&{\approx}&373.3[V]
\end{eqnarray}
上記のピーク値\(V_{INPEAK(MAX)}\)に対してディレーティングを考慮します。ディレーティングを80%とした場合、必要定格電圧\(V_{RATED}\)は以下の値となります。
\begin{eqnarray}
V_{RATED}&=&\frac{V_{INPEAK(MAX)}}{0.8}\\
&{\approx}&466.7[V]
\end{eqnarray}
上記より、600V品を選定します。信頼性を向上させるために、800V品～1000V品を使用してもよいと思います。

定格電流

ブリッジダイオードの後段にPFC回路を接続する場合と接続しない場合で計算方法が異なります。今回はPFC回路を接続しない場合における定格電流を計算します(PFC回路を使用した場合の計算方法についてはこの記事の後半に記載しています)。

ブリッジダイオードの必要定格電流\(I_{RATED}\)は『ブリッジダイオードに流れる電流の平均値』にディレーティングを考慮して決定します。

『ブリッジダイオードに流れる電流の平均値』は『入力電解コンデンサに流れる電流の平均値(または、入力AC電流の平均値)』と等しくなります。

ここで、コンバータの入力電力\(P_{CIN}\)は以下の値となります。
\begin{eqnarray}
P_{CIN}&=&\frac{P_{OUT}}{{\eta}_1}\\
&=&\frac{100}{0.9}\\
&{\approx}&111.1[W]
\end{eqnarray}

入力電解コンデンサにかかる電圧\(V_{CIN}\)が最小値\(V_{CIN(MIN)}\)となるときに、入力電解コンデンサに流れる電流の平均値が最大値\(I_{CINAVE(MAX)}\)となります。入力電解コンデンサにかかる電圧\(V_{CIN}\)の最小値\(V_{CIN(MIN)}\)は、入力AC電圧の最小値\(V_{INRMS (MIN)}\)のピーク値\(V_{INPEAK(MIN)}\)に対して、ブリッジダイオードの順方向電圧\(V_F\)を引いた値となるため、以下の値となります。
\begin{eqnarray}
V_{CIN(MIN)}&=&V_{INPEAK(MIN)}-2V_F\\
&=&V_{INRMS(MIN)}×\sqrt{2}-2V_F\\
&=&85×\sqrt{2}-2×0.7\\
&{\approx}&118.8[V]
\end{eqnarray}
したがって、入力電解コンデンサに流れる電流の平均値の最大値\(I_{CINAVE(MAX)}\)は以下の値となります。
\begin{eqnarray}
I_{CINAVE(MAX)}&=&\frac{P_{CIN}}{V_{CIN(MIN)}}\\
&{\approx}&\frac{111.1}{118.8}\\
&{\approx}&0.935[A]
\end{eqnarray}

上記の最大値\(I_{CINAVE(MAX)}\)に対してディレーティングを考慮します。ディレーティングを80%とした場合、必要定格電流\(I_{RATED}\)は以下の値となります。
\begin{eqnarray}
I_{RATED}&=&\frac{I_{CINAVE(MAX)}}{0.8}\\
&{\approx}&\frac{0.935}{0.8}\\
&{\approx}&1.17[A]
\end{eqnarray}
上記より、1.17Aより高い定格電流の素子を選定します。サージ電流に対して信頼性を向上させるために、入力電解コンデンサに流れる電流の平均値の最大値\(I_{CINAVE(MAX)}\)の2倍の余裕を持った素子を選定してもよいと思います。

サージ電流

必要定格電圧\(V_{RATED}\)と必要定格電流\(I_{RATED}\)を満たすダイオードを選定します。

選定したダイオードのデータシートを見ると、ピーク電流(またはせん頭サージ順電流)が記載されています。このピーク電流が電源の突入電流仕様値に対して十分に余裕があることを確認します。なお、電源の突入電流仕様値は突入防止回路によって決まります。突入防止回路については後日記事を書きます。

消費電力と昇温

ブリッジダイオードの順方向電圧\(V_F\)とブリッジダイオードに流れる平均電流の最大値\(I_{CINAVE(MAX)}\)から消費電力\(P_{LOSS}\)を計算します。ブリッジ整流なので、ブリッジダイオード内部のダイオード2個が同時に導通するため、消費電力\(P_{LOSS}\)は以下の式で表されます。
\begin{eqnarray}
P_{LOSS}&=&2×I_{CINAVE(MAX)}×V_F \\
&{\approx}&2×0.935×0.7\\
&{\approx}&1.31[W]
\end{eqnarray}

例えば、ブリッジダイオードの熱抵抗(放熱器なし)\({\theta}_{JA}\)が40℃/Wの場合、接合部(ジャンクション)の温度\(T_J\)と周囲温度\(T_A\)の温度差\({\Delta}T\)は以下の値となります。
\begin{eqnarray}
{\Delta}T&=&P_{LOSS}×{\theta}_{JA}\\
&{\approx}&1.31×40\\
&{\approx}&52.4[℃]
\end{eqnarray}

周囲温度が60℃の場合、接合部の温度\(T_J\)は\(60℃+52.4℃=112.4℃\)となります。この温度が接合部の温度\(T_J\)の絶対最大定格に対して余裕があることが必要です。

【その他】PFC回路を用いる場合

『ブリッジダイオードに流れる電流の平均値』は『入力AC電流の平均値\(I_{INAVE}\)』と等しくなります。

入力電力\(P_{IN}\)を計算します。出力電力\(P_{OUT}=100W\)、効率(電源全体)\({\eta}_2=0.85\)の場合、入力電力\(P_{IN}\)は以下の値となります。
\begin{eqnarray}
P_{IN}&=&\frac{P_{OUT}}{{\eta}_2}\\
&=&\frac{100}{0.85}\\
&{\approx}&117.6[W]
\end{eqnarray}

次に皮相電力\(S\)を計算します。電源の力率\({\cos}{\varphi}\)を0.9とすると、皮相電力\(S\)は以下の値となります。
\begin{eqnarray}
S&=&\frac{P_{IN}}{{\cos}{\varphi}}\\
&{\approx}&\frac{117.6}{0.9}\\
&{\approx}&130.7[VA]
\end{eqnarray}

入力AC電流の最大値\(I_{INRMS(MAX)}\)を計算します。入力AC電圧が最小値\(V_{INRMS(MIN)}\)の時に、入力AC電流は最大値\(I_{INRMS(MAX)}\)となるため、以下の値となります。
\begin{eqnarray}
I_{INRMS(MAX)}&=&\frac{S}{V_{INRMS(MIN)}}\\
&{\approx}&\frac{130.7}{85}\\
&{\approx}&1.53[A]
\end{eqnarray}

PFC回路を接続しているため、入力AC電流を正弦波と仮定すると、入力AC電流のピーク電流\(I_{INPEAK(MAX))}\)は以下の値となります。
\begin{eqnarray}
I_{INPEAK(MAX)}&=&I_{INRMS(MAX)}×\sqrt{2}\\
&{\approx}&1.53×\sqrt{2}\\
&{\approx}&2.17[A]
\end{eqnarray}

従って、入力AC電流の平均値(最大)\(I_{INAVE(MAX))}\)は以下の値となります。
\begin{eqnarray}
I_{INAVE(MAX)}&=&\frac{2}{{\pi}}I_{INPEAK(MAX)}\\
&{\approx}&\frac{2}{{\pi}}×2.17\\
&{\approx}&1.38[A]
\end{eqnarray}

上記の値に対してディレーティングを考慮します。ディレーティングを80%とした場合、必要定格電流\(I_{RATED}\)は以下の値となります。
\begin{eqnarray}
I_{RATED}&=&\frac{I_{INAVE(MAX))}}{0.8}\\
&{\approx}&\frac{1.38}{0.8}\\
&{\approx}&1.73[A]
\end{eqnarray}