ラプラス変換の「一覧表・変換表」と「証明」

この記事では『ラプラス変換』について

• ラプラス変換の「一覧表・変換表」
• ラプラス変換の「一覧表・変換表」の証明方法

などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。

ラプラス変換の一覧表・変換表

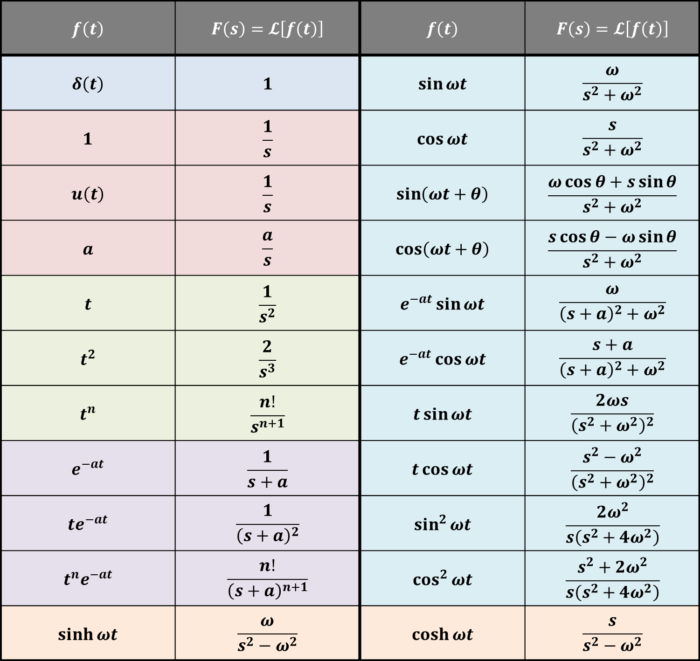
上図に示しているのは、ラプラス変換の「一覧表・変換表(\(f(t)\)と\(F(s)\)の関係)」です。

例えば、「\(f(t)=1\)」をラプラス変換すると「\(F(s)=\displaystyle\frac{1}{s}\)」になるということを示しています。

この記事では上図に示しているラプラス変換の「一覧表・変換表(\(f(t)\)と\(F(s)\)の関係)」の証明方法を説明しています。

ラプラス変換の一覧表・変換表の証明方法

ラプラス変換の一覧表・変換表(\(f(t)\)と\(F(s)\)の関係)は下記の定義式を用いることで証明することができます。

上式は時間\(t\)の関数\(f(t)\)に\(e^{-st}\)を掛けたものを\(t=0\)から\({\infty}\)まで積分すると、\(s\)の関数\(F(s)\)に変換できるということを示しています。

また、上式の記号\(\displaystyle\mathcal{L}\)はラプラス変換を表す記号です。\(\displaystyle\mathcal{L}\left[f(t)\right]\)と書くと、時間\(t\)の関数\(f(t)\)をラプラス変換するということになります。なお、\(\displaystyle\mathcal{L}\)はラプラス(Laplace)の頭文字を筆記体で書いたものです。

ではこれから、ラプラス変換の一覧表・変換表(\(f(t)\)と\(F(s)\)の関係)の証明方法について説明します。

「\(1\)」のラプラス変換

「\(f(t)=1\)」のラプラス変換\(F(s)\)を次式に示します。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[1\right]=\frac{1}{s}\tag{1-1}
\end{eqnarray}

証明方法

ラプラス変換の定義式に「\(f(t)=1\)」を代入して、計算すると、(1-1)式を証明することができます。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&{\displaystyle\int}_0^{\infty}f(t){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}1{\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&-\frac{1}{s}\left[e^{-st}\right]_0^{\infty}\\
\\
&=&-\frac{1}{s}\left(e^{-s{\;}{\cdot}{\;}{\infty}}-e^{-s{\;}{\cdot}{\;}0}\right)\\
\\
&=&-\frac{1}{s}\left(0-1\right)\\
\\
&=&\frac{1}{s}\tag{1-2}
\end{eqnarray}

単位ステップ関数「\(u(t)\)」のラプラス変換

次式に示すように、「\(f(t)=u(t)=1{\;}(t{≥}0)\)」で表される関数を単位ステップ関数といいます。

\begin{eqnarray}
u(t)=
\begin{cases}
0&(t{<}0)\\
1&(t{≥}0)
\end{cases}
\tag{2-1}
\end{eqnarray}

単位ステップ関数「\(f(t)=u(t)\)」のラプラス変換\(F(s)\)を次式に示します。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[u(t)\right]=\frac{1}{s}\tag{2-2}
\end{eqnarray}

証明方法

ラプラス変換の定義式に「\(f(t)=u(t)\)」を代入して、計算すると、(2-2)式を証明することができます。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&{\displaystyle\int}_0^{\infty}f(t){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}u(t){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}1{\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&-\frac{1}{s}\left[e^{-st}\right]_0^{\infty}\\
\\
&=&-\frac{1}{s}\left(e^{-s{\;}{\cdot}{\;}{\infty}}-e^{-s{\;}{\cdot}{\;}0}\right)\\
\\
&=&-\frac{1}{s}\left(0-1\right)\\
\\
&=&\frac{1}{s}\tag{2-3}
\end{eqnarray}

「\(a\)」のラプラス変換

「\(f(t)=a\)」のラプラス変換\(F(s)\)を次式に示します。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[a\right]=\frac{a}{s}\tag{3-1}
\end{eqnarray}

証明方法

ラプラス変換の定義式に「\(f(t)=a\)」を代入して、計算すると、(3-1)式を証明することができます。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&{\displaystyle\int}_0^{\infty}f(t){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}a{\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&a{\displaystyle\int}_0^{\infty}e^{-st}dt\\
\\
&=&-\frac{a}{s}\left[e^{-st}\right]_0^{\infty}\\
\\
&=&-\frac{a}{s}\left(e^{-s{\;}{\cdot}{\;}{\infty}}-e^{-s{\;}{\cdot}{\;}0}\right)\\
\\
&=&-\frac{a}{s}\left(0-1\right)\\
\\
&=&\frac{a}{s}\tag{3-2}
\end{eqnarray}

ランプ関数「\(f(t)=t\)」のラプラス変換

次式に示すように、「\(f(t)=t{\;}(t{≥}0)\)」で表される関数をランプ関数といいます。

\begin{eqnarray}
f(t)=
\begin{cases}
0&(t{<}0)\\
t&(t{≥}0)
\end{cases}
\tag{4-1}
\end{eqnarray}

ランプ関数「\(f(t)=t\)」のラプラス変換\(F(s)\)を次式に示します。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[t\right]=\frac{1}{s^2}\tag{4-2}
\end{eqnarray}

証明方法

ラプラス変換の定義式に「\(f(t)=t\)」を代入すると、

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&{\displaystyle\int}_0^{\infty}f(t){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}t{\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}t{\;}{\cdot}{\;}\left(\frac{1}{-s}e^{-st}\right)'dt\tag{4-3}
\end{eqnarray}

のように変形することができます。ここで、部分積分の公式を用いると、次式となり、(4-2)式を証明することができます。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&{\displaystyle\int}_0^{\infty}t{\;}{\cdot}{\;}\left(\frac{1}{-s}e^{-st}\right)'dt\\
\\
&=&\left[t{\;}{\cdot}{\;}\left(\frac{1}{-s}e^{-st}\right)\right]_0^{\infty}-{\displaystyle\int}_0^{\infty}(t)'{\;}{\cdot}{\;}\left(\frac{1}{-s}e^{-st}\right)dt\\
\\
&=&0+\frac{1}{s}{\displaystyle\int}_0^{\infty}e^{-st}dt\\
\\
&=&-\frac{1}{s^2}\left[e^{-st}\right]_0^{\infty}\\
\\
&=&-\frac{1}{s^2}\left(e^{-s{\;}{\cdot}{\;}{\infty}}-e^{-s{\;}{\cdot}{\;}0}\right)\\
\\
&=&-\frac{1}{s^2}\left(0-1\right)\\
\\
&=&\frac{1}{s^2}\tag{4-4}
\end{eqnarray}

「\(t^2\)」のラプラス変換

「\(f(t)=t^2\)」のラプラス変換\(F(s)\)を次式に示します。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[t^2\right]=\frac{2}{s^3}\tag{5-1}
\end{eqnarray}

証明方法

ラプラス変換の定義式に「\(f(t)=t^2\)」を代入すると、

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&{\displaystyle\int}_0^{\infty}f(t){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}t^2{\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}t^2{\;}{\cdot}{\;}\left(\frac{1}{-s}e^{-st}\right)'dt\tag{5-2}
\end{eqnarray}

と変形することができます。ここで、部分積分の公式を用いると、

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&{\displaystyle\int}_0^{\infty}t^2{\;}{\cdot}{\;}\left(\frac{1}{-s}e^{-st}\right)'dt\\
\\
&=&\left[t^2{\;}{\cdot}{\;}\left(\frac{1}{-s}e^{-st}\right)\right]_0^{\infty}-{\displaystyle\int}_0^{\infty}(t^2)'{\;}{\cdot}{\;}\left(\frac{1}{-s}e^{-st}\right)dt\\
\\
&=&0+\frac{2}{s}{\displaystyle\int}_0^{\infty}t{\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&\frac{2}{s}{\displaystyle\int}_0^{\infty}t{\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&\frac{2}{s}\displaystyle\mathcal{L}\left[t\right]\tag{5-3}
\end{eqnarray}

のように変形することができます。

ここで、(4-2)式の「\(\displaystyle\mathcal{L}\left[t\right]=\displaystyle\frac{1}{s^2}\)」を(5-3)式に代入すると、次式となり、(5-1)式を証明することができます。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&\frac{2}{s}\displaystyle\mathcal{L}\left[t\right]\\
\\
&=&\frac{2}{s}{\;}{\cdot}{\;}\frac{1}{s^2}\\
\\
&=&\frac{2}{s^3}\tag{5-4}
\end{eqnarray}

「\(t^n\)」のラプラス変換

「\(f(t)=t^n\)」のラプラス変換\(F(s)\)を次式に示します。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[t^n\right]=\frac{n!}{s^{n+1}}\tag{6-1}
\end{eqnarray}

証明方法

「\(\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[t^n\right]=\displaystyle\frac{n!}{s^{n+1}}\)」が成り立つことを、数学的帰納法を用いて証明します。

すると、「\(n=k+1\)」のとき、ラプラス変換の定義式より、

\begin{eqnarray}
\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[t^{k+1}\right]&=&{\displaystyle\int}_0^{\infty}t^{k+1}{\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}t^{k+1}{\;}{\cdot}{\;}\left(\frac{1}{-s}e^{-st}\right)'dt\tag{6-4}
\end{eqnarray}

のように変形することができます。ここで、部分積分の公式を用いると、(6-4)式は次式となります。

\begin{eqnarray}
\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[t^{k+1}\right]&=&{\displaystyle\int}_0^{\infty}t^{k+1}{\;}{\cdot}{\;}\left(\frac{1}{-s}e^{-st}\right)'dt\\
\\
&=&\left[t^{k+1}{\;}{\cdot}{\;}\left(\frac{1}{-s}e^{-st}\right)\right]_0^{\infty}-{\displaystyle\int}_0^{\infty}(t^{k+1})'{\;}{\cdot}{\;}\left(\frac{1}{-s}e^{-st}\right)dt\\
\\
&=&0-{\displaystyle\int}_0^{\infty}(k+1)t^k{\;}{\cdot}{\;}\left(\frac{1}{-s}e^{-st}\right)dt\\
\\
&=&\frac{k+1}{s}{\displaystyle\int}_0^{\infty}t^k{\;}{\cdot}{\;}e^{-st}dt\tag{6-5}
\end{eqnarray}

ここで、(6-3)式の「\(\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[t^k\right]={\displaystyle\int}_0^{\infty}t^k{\;}{\cdot}{\;}e^{-st}dt=\displaystyle\frac{k!}{s^{k+1}}\)」の仮定を用いると、(6-5)式は、

\begin{eqnarray}
\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[t^{k+1}\right]&=&\frac{k+1}{s}{\displaystyle\int}_0^{\infty}t^k{\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&\frac{k+1}{s}{\;}{\cdot}{\;}\frac{k!}{s^{k+1}}\\
\\
&=&\frac{(k+1)!}{s^{(k+1)+1}}\tag{6-6}
\end{eqnarray}

となるため、「\(n=k+1\)」のときも成り立ちます。

したがって、数学的帰納法より、「\(n=0,1,2,…\)」のとき、

\begin{eqnarray}
\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[t^n\right]=\frac{n!}{s^{n+1}}\tag{6-7}
\end{eqnarray}

が成り立ちます。

「\(e^{-at}\)」のラプラス変換

「\(f(t)=e^{-at}\)」のラプラス変換\(F(s)\)を次式に示します。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[e^{-at}\right]=\frac{1}{s+a}\tag{7-1}
\end{eqnarray}

証明方法

ラプラス変換の定義式に「\(f(t)=e^{-at}\)」を代入して、計算すると、(7-1)式を証明することができます。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&{\displaystyle\int}_0^{\infty}f(t){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}e^{-at}{\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}e^{-(s+a)t}dt\\
\\
&=&-\frac{1}{s+a}\left[e^{-(s+a)t}\right]_0^{\infty}\\
\\
&=&-\frac{1}{s+a}\left(e^{-(s+a){\;}{\cdot}{\;}{\infty}}-e^{-(s+a){\;}{\cdot}{\;}0}\right)\\
\\
&=&-\frac{1}{s+a}\left(0-1\right)\\
\\
&=&\frac{1}{s+a}\tag{7-2}
\end{eqnarray}

「\(te^{-at}\)」のラプラス変換

「\(f(t)=te^{-at}\)」のラプラス変換\(F(s)\)を次式に示します。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[te^{-at}\right]=\frac{1}{(s+a)^2}\tag{8-1}
\end{eqnarray}

証明方法

ラプラス変換の定義式に「\(f(t)=te^{-at}\)」を代入すると、

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&{\displaystyle\int}_0^{\infty}f(t){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}te^{-at}{\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}te^{-(s+a)t}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}t{\;}{\cdot}{\;}\left(\frac{1}{-(s+a)}e^{-(s+a)t}\right)'dt\tag{8-2}
\end{eqnarray}

のように変形することができます。ここで、部分積分の公式を用いると、次式となり、(8-1)式を証明することができます。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&{\displaystyle\int}_0^{\infty}t{\;}{\cdot}{\;}\left(\frac{1}{-(s+a)}e^{-(s+a)t}\right)'dt\\
\\
&=&\left[t{\;}{\cdot}{\;}\left(\frac{1}{-(s+a)}e^{-(s+a)t}\right)\right]_0^{\infty}-{\displaystyle\int}_0^{\infty}(t)'{\;}{\cdot}{\;}\left(\frac{1}{-(s+a)}e^{-(s+a)t}\right)dt\\
\\
&=&0+\frac{1}{s+a}{\displaystyle\int}_0^{\infty}e^{-(s+a)t}dt\\
\\
&=&-\frac{1}{(s+a)^2}\left[e^{-(s+a)t}\right]_0^{\infty}\\
\\
&=&-\frac{1}{(s+a)^2}\left\{e^{-(s+a){\;}{\cdot}{\;}{\infty}}-e^{-(s+a){\;}{\cdot}{\;}0}\right\}\\
\\
&=&-\frac{1}{(s+a)^2}\left(0-1\right)\\
\\
&=&\frac{1}{(s+a)^2}\tag{8-3}
\end{eqnarray}

「\(t^ne^{-at}\)」のラプラス変換

「\(f(t)=t^ne^{-at}\)」のラプラス変換\(F(s)\)を次式に示します。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[t^ne^{-at}\right]=\frac{n!}{(s+a)^{n+1}}\tag{9-1}
\end{eqnarray}

証明方法

「\(\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[t^ne^{-at}\right]=\displaystyle\frac{n!}{(s+a)^{n+1}}\)」が成り立つことを、数学的帰納法を用いて証明します。

すると、「\(n=k+1\)」のとき、ラプラス変換の定義式より、

\begin{eqnarray}
\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[t^{k+1}e^{-at}\right]&=&{\displaystyle\int}_0^{\infty}t^{k+1}e^{-at}{\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}t^{k+1}e^{-(s+a)t}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}t^{k+1}{\;}{\cdot}{\;}\left(\frac{1}{-(s+a)}e^{-(s+a)t}\right)'dt\tag{9-4}
\end{eqnarray}

のように変形することができます。ここで、部分積分の公式を用いると、(9-4)式は次式となります。

\begin{eqnarray}
\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[t^{k+1}e^{-at}\right]&=&{\displaystyle\int}_0^{\infty}t^{k+1}{\;}{\cdot}{\;}\left(\frac{1}{-(s+a)}e^{-(s+a)t}\right)'dt\\
\\
&=&\left[t^{k+1}{\;}{\cdot}{\;}\left(\frac{1}{-(s+a)}e^{-(s+a)t}\right)\right]_0^{\infty}-{\displaystyle\int}_0^{\infty}(t^{k+1})'{\;}{\cdot}{\;}\left(\frac{1}{-(s+a)}e^{-(s+a)t}\right)dt\\
\\
&=&0-{\displaystyle\int}_0^{\infty}(k+1)t^k{\;}{\cdot}{\;}\left(\frac{1}{-(s+a)}e^{-(s+a)t}\right)dt\\
\\
&=&\frac{k+1}{s+a}{\displaystyle\int}_0^{\infty}t^k{\;}{\cdot}{\;}e^{-(s+a)t}dt\tag{9-5}
\end{eqnarray}

ここで、(9-3)式の「\(\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[t^ke^{-at}\right]={\displaystyle\int}_0^{\infty}t^ke^{-at}{\;}{\cdot}{\;}e^{-st}dt=\displaystyle\frac{k!}{(s+a)^{k+1}}\)」の仮定を用いると、(9-5)式は、

\begin{eqnarray}
\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[t^{k+1}e^{-at}\right]&=&\frac{k+1}{s+a}{\displaystyle\int}_0^{\infty}t^k{\;}{\cdot}{\;}e^{-(s+a)t}dt\\
\\
&=&\frac{k+1}{s+a}{\;}{\cdot}{\;}\frac{k!}{(s+a)^{k+1}}\\
\\
&=&\frac{(k+1)!}{(s+a)^{(k+1)+1}}\tag{9-6}
\end{eqnarray}

となるため、「\(n=k+1\)」のときも成り立ちます。

したがって、数学的帰納法より、「\(n=0,1,2,…\)」のとき、

\begin{eqnarray}
\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[t^ne^{-at}\right]=\frac{n!}{(s+a)^{n+1}}\tag{9-7}
\end{eqnarray}

が成り立ちます。

「\({\sin}{\omega}t\)」のラプラス変換

「\(f(t)={\sin}{\omega}t\)」のラプラス変換\(F(s)\)を次式に示します。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[{\sin}{\omega}t\right]=\frac{{\omega}}{s^2+{\omega}^2}\tag{10-1}
\end{eqnarray}

証明方法

まず、「\(f(t)={\sin}{\omega}t\)」を「\(f(t)=e^■\)」の形に変形させます。

オイラーの公式より次式が成り立ちます。

\begin{eqnarray}
e^{j{\omega}t}&=&{\cos}{\omega}t+j{\sin}{\omega}t\tag{10-2}\\
\\
e^{-j{\omega}t}&=&{\cos}{\omega}t-j{\sin}{\omega}t\tag{10-3}
\end{eqnarray}

上式を用いると、「\(f(t)={\sin}{\omega}t\)」は次式のように変形することができます。

\begin{eqnarray}
f(t)={\sin}{\omega}t=\frac{1}{2j}(e^{j{\omega}t}-e^{-j{\omega}t})\tag{10-4}
\end{eqnarray}

以上より、ラプラス変換の定義式に「\(f(t)={\sin}{\omega}t\)」を代入すると、

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&{\displaystyle\int}_0^{\infty}f(t){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}{\sin}{\omega}t{\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}\frac{1}{2j}(e^{j{\omega}t}-e^{-j{\omega}t}){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&\frac{1}{2j}\left({\displaystyle\int}_0^{\infty}e^{j{\omega}t}{\;}{\cdot}{\;}e^{-st}dt-{\displaystyle\int}_0^{\infty}e^{-j{\omega}t}{\;}{\cdot}{\;}e^{-st}dt\right)
\\
&=&\frac{1}{2j}\left(\displaystyle\mathcal{L}\left[e^{j{\omega}t}\right]-\displaystyle\mathcal{L}\left[e^{-j{\omega}t}\right]\right)\tag{10-5}
\end{eqnarray}

のように変形することができます。

ここで、(7-1)式より、「\(\displaystyle\mathcal{L}\left[e^{-at}\right]=\displaystyle\frac{1}{s+a}\)」なので、\(\displaystyle\mathcal{L}\left[e^{j{\omega}t}\right]\)と\(\displaystyle\mathcal{L}\left[e^{-j{\omega}t}\right]\)は次式で表されます。

\begin{eqnarray}
\displaystyle\mathcal{L}\left[e^{j{\omega}t}\right]&=&\frac{1}{s-j{\omega}}\tag{10-6}\\
\\
\displaystyle\mathcal{L}\left[e^{-j{\omega}t}\right]&=&\frac{1}{s+j{\omega}}\tag{10-7}
\end{eqnarray}

(10-6)式と(10-7)式を(10-5)式に代入すると、次式のようになり、「\(f(t)={\sin}{\omega}t\)」のラプラス変換\(F(s)\)を導出することができます。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&\frac{1}{2j}\left(\displaystyle\mathcal{L}\left[e^{j{\omega}t}\right]-\displaystyle\mathcal{L}\left[e^{-j{\omega}t}\right]\right)\\
\\
&=&\frac{1}{2j}\left(\frac{1}{s-j{\omega}}-\frac{1}{s+j{\omega}}\right)\\
\\
&=&\frac{1}{2j}\left(\frac{s+j{\omega}}{s^2+{\omega}^2}-\frac{s-j{\omega}}{s^2+{\omega}^2}\right)\\
\\
&=&\frac{{\omega}}{s^2+{\omega}^2}\tag{10-8}
\end{eqnarray}

「\({\cos}{\omega}t\)」のラプラス変換

「\(f(t)={\cos}{\omega}t\)」のラプラス変換\(F(s)\)を次式に示します。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[{\cos}{\omega}t\right]=\frac{s}{s^2+{\omega}^2}\tag{11-1}
\end{eqnarray}

証明方法

まず、「\(f(t)={\cos}{\omega}t\)」を「\(f(t)=e^■\)」の形に変形させます。

オイラーの公式より次式が成り立ちます。

\begin{eqnarray}
e^{j{\omega}t}&=&{\cos}{\omega}t+j{\sin}{\omega}t\tag{11-2}\\
\\
e^{-j{\omega}t}&=&{\cos}{\omega}t-j{\sin}{\omega}t\tag{11-3}
\end{eqnarray}

上式を用いると、「\(f(t)={\cos}{\omega}t\)」は次式のように変形することができます。

\begin{eqnarray}
f(t)={\cos}{\omega}t=\frac{1}{2}(e^{j{\omega}t}+e^{-j{\omega}t})\tag{11-4}
\end{eqnarray}

以上より、ラプラス変換の定義式に「\(f(t)={\cos}{\omega}t\)」を代入すると、

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&{\displaystyle\int}_0^{\infty}f(t){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}{\cos}{\omega}t{\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}\frac{1}{2}(e^{j{\omega}t}+e^{-j{\omega}t}){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&\frac{1}{2}\left({\displaystyle\int}_0^{\infty}e^{j{\omega}t}{\;}{\cdot}{\;}e^{-st}dt+{\displaystyle\int}_0^{\infty}e^{-j{\omega}t}{\;}{\cdot}{\;}e^{-st}dt\right)
\\
&=&\frac{1}{2}\left(\displaystyle\mathcal{L}\left[e^{j{\omega}t}\right]+\displaystyle\mathcal{L}\left[e^{-j{\omega}t}\right]\right)\tag{11-5}
\end{eqnarray}

のように変形することができます。

ここで、(7-1)式より、「\(\displaystyle\mathcal{L}\left[e^{-at}\right]=\displaystyle\frac{1}{s+a}\)」なので、\(\displaystyle\mathcal{L}\left[e^{j{\omega}t}\right]\)と\(\displaystyle\mathcal{L}\left[e^{-j{\omega}t}\right]\)は次式で表されます。

\begin{eqnarray}
\displaystyle\mathcal{L}\left[e^{j{\omega}t}\right]&=&\frac{1}{s-j{\omega}}\tag{11-6}\\
\\
\displaystyle\mathcal{L}\left[e^{-j{\omega}t}\right]&=&\frac{1}{s+j{\omega}}\tag{11-7}
\end{eqnarray}

(11-6)式と(11-7)式を(11-5)式に代入すると、次式のようになり、「\(f(t)={\cos}{\omega}t\)」のラプラス変換\(F(s)\)を導出することができます。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&\frac{1}{2}\left(\displaystyle\mathcal{L}\left[e^{j{\omega}t}\right]+\displaystyle\mathcal{L}\left[e^{-j{\omega}t}\right]\right)\\
\\
&=&\frac{1}{2}\left(\frac{1}{s-j{\omega}}+\frac{1}{s+j{\omega}}\right)\\
\\
&=&\frac{1}{2}\left(\frac{s+j{\omega}}{s^2+{\omega}^2}+\frac{s-j{\omega}}{s^2+{\omega}^2}\right)\\
\\
&=&\frac{s}{s^2+{\omega}^2}\tag{11-8}
\end{eqnarray}

「\({\sin}({\omega}t+{\theta})\)」のラプラス変換

「\(f(t)={\sin}({\omega}t+{\theta})\)」のラプラス変換\(F(s)\)を次式に示します。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[{\sin}({\omega}t+{\theta})\right]=\frac{{\omega}{\cos}{\theta}+s{\sin}{\theta}}{s^2+{\omega}^2}\tag{12-1}
\end{eqnarray}

証明方法

加法定理を用いると、「\(f(t)={\sin}({\omega}t+{\theta})\)」のラプラス変換\(F(s)\)を導出することができます。

\(\displaystyle\mathcal{L}\left[{\sin}({\omega}t+{\theta})\right]\)に加法定理を用いると、次式のように変形することができます。

\begin{eqnarray}
\displaystyle\mathcal{L}\left[{\sin}({\omega}t+{\theta})\right]&=&\displaystyle\mathcal{L}\left[{\sin}{\omega}t{\cos}{\theta}+{\cos}{\omega}t{\sin}{\theta}\right]\\
\\
&=&\displaystyle\mathcal{L}\left[{\sin}{\omega}t{\cos}{\theta}\right]+\displaystyle\mathcal{L}\left[{\cos}{\omega}t{\sin}{\theta}\right]\\
\\
&=&{\cos}{\theta}{\;}{\cdot}{\;}\displaystyle\mathcal{L}\left[{\sin}{\omega}t\right]+{\sin}{\theta}{\;}{\cdot}{\;}\displaystyle\mathcal{L}\left[{\cos}{\omega}t\right]\tag{12-2}
\end{eqnarray}

ここで、(10-1)式と(11-1)式より、\(\displaystyle\mathcal{L}\left[{\sin}{\omega}t\right]\)と\(\displaystyle\mathcal{L}\left[{\cos}{\omega}t\right]\)は次式で表されます。

\begin{eqnarray}
\displaystyle\mathcal{L}\left[{\sin}{\omega}t\right]&=&\frac{{\omega}}{s^2+{\omega}^2}\tag{12-3}\\
\\
\displaystyle\mathcal{L}\left[{\cos}{\omega}t\right]&=&\frac{s}{s^2+{\omega}^2}\tag{12-4}
\end{eqnarray}

(12-3)式と(12-4)式を(12-2)式に代入すると、次式のようになり、「\(f(t)={\sin}({\omega}t+{\theta})\)」のラプラス変換\(F(s)\)を導出することができます。

\begin{eqnarray}
\displaystyle\mathcal{L}\left[{\sin}({\omega}t+{\theta})\right]&=&{\cos}{\theta}{\;}{\cdot}{\;}\displaystyle\mathcal{L}\left[{\sin}{\omega}t\right]+{\sin}{\theta}{\;}{\cdot}{\;}\displaystyle\mathcal{L}\left[{\cos}{\omega}t\right]\\
\\
&=&{\cos}{\theta}{\;}{\cdot}{\;}\frac{{\omega}}{s^2+{\omega}^2}+{\sin}{\theta}{\;}{\cdot}{\;}\frac{s}{s^2+{\omega}^2}\\
\\
&=&\frac{{\omega}{\cos}{\theta}+s{\sin}{\theta}}{s^2+{\omega}^2}\tag{12-5}
\end{eqnarray}

「\({\cos}({\omega}t+{\theta})\)」のラプラス変換

「\(f(t)={\cos}({\omega}t+{\theta})\)」のラプラス変換\(F(s)\)を次式に示します。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[{\cos}({\omega}t+{\theta})\right]=\frac{s{\cos}{\theta}-{\omega}{\sin}{\theta}}{s^2+{\omega}^2}\tag{13-1}
\end{eqnarray}

証明方法

加法定理を用いると、「\(f(t)={\cos}({\omega}t+{\theta})\)」のラプラス変換\(F(s)\)を導出することができます。

\(\displaystyle\mathcal{L}\left[{\cos}({\omega}t+{\theta})\right]\)に加法定理を用いると、次式のように変形することができます。

\begin{eqnarray}
\displaystyle\mathcal{L}\left[{\cos}({\omega}t+{\theta})\right]&=&\displaystyle\mathcal{L}\left[{\cos}{\omega}t{\cos}{\theta}-{\sin}{\omega}t{\sin}{\theta}\right]\\
\\
&=&\displaystyle\mathcal{L}\left[{\cos}{\omega}t{\cos}{\theta}\right]-\displaystyle\mathcal{L}\left[{\sin}{\omega}t{\sin}{\theta}\right]\\
\\
&=&{\cos}{\theta}{\;}{\cdot}{\;}\displaystyle\mathcal{L}\left[{\cos}{\omega}t\right]-{\sin}{\theta}{\;}{\cdot}{\;}\displaystyle\mathcal{L}\left[{\sin}{\omega}t\right]\tag{13-2}
\end{eqnarray}

ここで、(10-1)式と(11-1)式より、\(\displaystyle\mathcal{L}\left[{\sin}{\omega}t\right]\)と\(\displaystyle\mathcal{L}\left[{\cos}{\omega}t\right]\)は次式で表されます。

\begin{eqnarray}
\displaystyle\mathcal{L}\left[{\sin}{\omega}t\right]&=&\frac{{\omega}}{s^2+{\omega}^2}\tag{13-3}\\
\\
\displaystyle\mathcal{L}\left[{\cos}{\omega}t\right]&=&\frac{s}{s^2+{\omega}^2}\tag{13-4}
\end{eqnarray}

(13-3)式と(13-4)式を(13-2)式に代入すると、次式のようになり、「\(f(t)={\cos}({\omega}t+{\theta})\)」のラプラス変換\(F(s)\)を導出することができます。

\begin{eqnarray}
\displaystyle\mathcal{L}\left[{\cos}({\omega}t+{\theta})\right]&=&{\cos}{\theta}{\;}{\cdot}{\;}\displaystyle\mathcal{L}\left[{\cos}{\omega}t\right]-{\sin}{\theta}{\;}{\cdot}{\;}\displaystyle\mathcal{L}\left[{\sin}{\omega}t\right]\\
\\
&=&{\cos}{\theta}{\;}{\cdot}{\;}\frac{s}{s^2+{\omega}^2}-{\sin}{\theta}{\;}{\cdot}{\;}\frac{{\omega}}{s^2+{\omega}^2}\\
\\
&=&\frac{s{\cos}{\theta}-{\omega}{\sin}{\theta}}{s^2+{\omega}^2}\tag{13-5}
\end{eqnarray}

「\(e^{-at}{\sin}{\omega}t\)」のラプラス変換

「\(f(t)=e^{-at}{\sin}{\omega}t\)」のラプラス変換\(F(s)\)を次式に示します。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[e^{-at}{\sin}{\omega}t\right]=\frac{{\omega}}{(s+a)^2+{\omega}^2}\tag{14-1}
\end{eqnarray}

証明方法

まず、「\(f(t)=e^{-at}{\sin}{\omega}t\)」を「\(f(t)=e^■\)」の形に変形させます。

オイラーの公式より次式が成り立ちます。

\begin{eqnarray}
e^{j{\omega}t}&=&{\cos}{\omega}t+j{\sin}{\omega}t\tag{14-2}\\
\\
e^{-j{\omega}t}&=&{\cos}{\omega}t-j{\sin}{\omega}t\tag{14-3}
\end{eqnarray}

上式を用いると、「\(f(t)=e^{-at}{\sin}{\omega}t\)」は次式のように変形することができます。

\begin{eqnarray}
f(t)=e^{-at}{\sin}{\omega}t=e^{-at}{\;}{\cdot}{\;}\frac{1}{2j}(e^{j{\omega}t}-e^{-j{\omega}t})\tag{14-4}
\end{eqnarray}

以上より、ラプラス変換の定義式に「\(f(t)=e^{-at}{\sin}{\omega}t\)」を代入すると、

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&{\displaystyle\int}_0^{\infty}f(t){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}e^{-at}{\sin}{\omega}t{\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}e^{-at}{\;}{\cdot}{\;}\frac{1}{2j}(e^{j{\omega}t}-e^{-j{\omega}t}){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&\frac{1}{2j}\left({\displaystyle\int}_0^{\infty}e^{(j{\omega}-a)t}{\;}{\cdot}{\;}e^{-st}dt-{\displaystyle\int}_0^{\infty}e^{-(j{\omega}+a)t}{\;}{\cdot}{\;}e^{-st}dt\right)
\\
&=&\frac{1}{2j}\left(\displaystyle\mathcal{L}\left[e^{(j{\omega}-a)t}\right]-\displaystyle\mathcal{L}\left[e^{-(j{\omega}+a)t}\right]\right)\tag{14-5}
\end{eqnarray}

のように変形することができます。

ここで、(7-1)式より、「\(\displaystyle\mathcal{L}\left[e^{-at}\right]=\displaystyle\frac{1}{s+a}\)」なので、\(\displaystyle\mathcal{L}\left[e^{(j{\omega}-a)t}\right]\)と\(\displaystyle\mathcal{L}\left[e^{-(j{\omega}+a)t}\right]\)は次式で表されます。

\begin{eqnarray}
\displaystyle\mathcal{L}\left[e^{(j{\omega}-a)t}\right]&=&\frac{1}{s-(j{\omega}-a)}=\frac{1}{(s+a)-j{\omega}}\tag{14-6}\\
\\
\displaystyle\mathcal{L}\left[e^{-(j{\omega}+a)t}\right]&=&\frac{1}{s+(j{\omega}+a)}=\frac{1}{(s+a)+j{\omega}}\tag{14-7}
\end{eqnarray}

(14-6)式と(14-7)式を(14-5)式に代入すると、次式のようになり、「\(f(t)=e^{-at}{\sin}{\omega}t\)」のラプラス変換\(F(s)\)を導出することができます。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&\frac{1}{2j}\left(\displaystyle\mathcal{L}\left[e^{(j{\omega}-a)t}\right]-\displaystyle\mathcal{L}\left[e^{-(j{\omega}+a)t}\right]\right)\\
\\
&=&\frac{1}{2j}\left\{(\frac{1}{(s+a)-j{\omega}}-\frac{1}{(s+a)+j{\omega}}\right\}\\
\\
&=&\frac{1}{2j}\left\{\frac{(s+a)+j{\omega}}{(s+a)^2+{\omega}^2}-\frac{(s+a)-j{\omega}}{(s+a)^2+{\omega}^2}\right\}\\
\\
&=&\frac{{\omega}}{(s+a)^2+{\omega}^2}\tag{14-8}
\end{eqnarray}

「\(e^{-at}{\cos}{\omega}t\)」のラプラス変換

「\(f(t)=e^{-at}{\cos}{\omega}t\)」のラプラス変換\(F(s)\)を次式に示します。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[e^{-at}{\cos}{\omega}t\right]=\frac{s+a}{(s+a)^2+{\omega}^2}\tag{15-1}
\end{eqnarray}

証明方法

まず、「\(f(t)=e^{-at}{\cos}{\omega}t\)」を「\(f(t)=e^■\)」の形に変形させます。

オイラーの公式より次式が成り立ちます。

\begin{eqnarray}
e^{j{\omega}t}&=&{\cos}{\omega}t+j{\sin}{\omega}t\tag{15-2}\\
\\
e^{-j{\omega}t}&=&{\cos}{\omega}t-j{\sin}{\omega}t\tag{15-3}
\end{eqnarray}

上式を用いると、「\(f(t)=e^{-at}{\cos}{\omega}t\)」は次式のように変形することができます。

\begin{eqnarray}
f(t)=e^{-at}{\cos}{\omega}t=e^{-at}{\;}{\cdot}{\;}\frac{1}{2}(e^{j{\omega}t}+e^{-j{\omega}t})\tag{15-4}
\end{eqnarray}

以上より、ラプラス変換の定義式に「\(f(t)=e^{-at}{\cos}{\omega}t\)」を代入すると、

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&{\displaystyle\int}_0^{\infty}f(t){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}e^{-at}{\cos}{\omega}t{\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}e^{-at}{\;}{\cdot}{\;}\frac{1}{2}(e^{j{\omega}t}+e^{-j{\omega}t}){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&\frac{1}{2}\left({\displaystyle\int}_0^{\infty}e^{(j{\omega}-a)t}{\;}{\cdot}{\;}e^{-st}dt+{\displaystyle\int}_0^{\infty}e^{-(j{\omega}+a)t}{\;}{\cdot}{\;}e^{-st}dt\right)
\\
&=&\frac{1}{2}\left(\displaystyle\mathcal{L}\left[e^{(j{\omega}-a)t}\right]+\displaystyle\mathcal{L}\left[e^{-(j{\omega}+a)t}\right]\right)\tag{15-5}
\end{eqnarray}

のように変形することができます。

ここで、(7-1)式より、「\(\displaystyle\mathcal{L}\left[e^{-at}\right]=\displaystyle\frac{1}{s+a}\)」なので、\(\displaystyle\mathcal{L}\left[e^{(j{\omega}-a)t}\right]\)と\(\displaystyle\mathcal{L}\left[e^{-(j{\omega}+a)t}\right]\)は次式で表されます。

\begin{eqnarray}
\displaystyle\mathcal{L}\left[e^{(j{\omega}-a)t}\right]&=&\frac{1}{s-(j{\omega}-a)}=\frac{1}{(s+a)-j{\omega}}\tag{15-6}\\
\\
\displaystyle\mathcal{L}\left[e^{-(j{\omega}+a)t}\right]&=&\frac{1}{s+(j{\omega}+a)}=\frac{1}{(s+a)+j{\omega}}\tag{15-7}
\end{eqnarray}

(15-6)式と(15-7)式を(15-5)式に代入すると、次式のようになり、「\(f(t)=e^{-at}{\cos}{\omega}t\)」のラプラス変換\(F(s)\)を導出することができます。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&\frac{1}{2}\left(\displaystyle\mathcal{L}\left[e^{(j{\omega}-a)t}\right]+\displaystyle\mathcal{L}\left[e^{-(j{\omega}+a)t}\right]\right)\\
\\
&=&\frac{1}{2}\left\{\frac{1}{(s+a)-j{\omega}}+\frac{1}{(s+a)+j{\omega}}\right\}\\
\\
&=&\frac{1}{2}\left\{\frac{(s+a)+j{\omega}}{(s+a)^2+{\omega}^2}+\frac{(s+a)-j{\omega}}{(s+a)^2+{\omega}^2}\right\}\\
\\
&=&\frac{s+a}{(s+a)^2+{\omega}^2}\tag{15-8}
\end{eqnarray}

「\(t{\sin}{\omega}t\)」のラプラス変換

「\(f(t)=t{\sin}{\omega}t\)」のラプラス変換\(F(s)\)を次式に示します。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[t{\sin}{\omega}t\right]=\frac{2{\omega}s}{(s^2+{\omega}^2)^2}\tag{16-1}
\end{eqnarray}

証明方法

まず、「\(f(t)=t{\sin}{\omega}t\)」を「\(f(t)=e^■\)」の形に変形させます。

オイラーの公式より次式が成り立ちます。

\begin{eqnarray}
e^{j{\omega}t}&=&{\cos}{\omega}t+j{\sin}{\omega}t\tag{16-2}\\
\\
e^{-j{\omega}t}&=&{\cos}{\omega}t-j{\sin}{\omega}t\tag{16-3}
\end{eqnarray}

上式を用いると、「\(f(t)=t{\sin}{\omega}t\)」は次式のように変形することができます。

\begin{eqnarray}
f(t)=t{\sin}{\omega}t=t{\;}{\cdot}{\;}\frac{1}{2j}(e^{j{\omega}t}-e^{-j{\omega}t})\tag{16-4}
\end{eqnarray}

以上より、ラプラス変換の定義式に「\(f(t)=t{\sin}{\omega}t\)」を代入すると、

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&{\displaystyle\int}_0^{\infty}f(t){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}t{\sin}{\omega}t{\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}t{\;}{\cdot}{\;}\frac{1}{2j}(e^{j{\omega}t}-e^{-j{\omega}t}){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&\frac{1}{2j}\left({\displaystyle\int}_0^{\infty}te^{j{\omega}t}{\;}{\cdot}{\;}e^{-st}dt-{\displaystyle\int}_0^{\infty}te^{-j{\omega}t}{\;}{\cdot}{\;}e^{-st}dt\right)
\\
&=&\frac{1}{2j}\left(\displaystyle\mathcal{L}\left[te^{j{\omega}t}\right]-\displaystyle\mathcal{L}\left[te^{-j{\omega}t}\right]\right)\tag{16-5}
\end{eqnarray}

のように変形することができます。

ここで、(8-1)式より、「\(\displaystyle\mathcal{L}\left[te^{-at}\right]=\displaystyle\frac{1}{(s+a)^2}\)」なので、\(\displaystyle\mathcal{L}\left[te^{j{\omega}t}\right]\)と\(\displaystyle\mathcal{L}\left[te^{-j{\omega}t}\right]\)は次式で表されます。

\begin{eqnarray}
\displaystyle\mathcal{L}\left[te^{j{\omega}t}\right]&=&\frac{1}{(s-j{\omega})^2}\tag{16-6}\\
\\
\displaystyle\mathcal{L}\left[te^{-j{\omega}t}\right]&=&\frac{1}{(s+j{\omega})^2}\tag{16-7}
\end{eqnarray}

(16-6)式と(16-7)式を(16-5)式に代入すると、次式のようになり、「\(f(t)=t{\sin}{\omega}t\)」のラプラス変換\(F(s)\)を導出することができます。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&\frac{1}{2j}\left(\displaystyle\mathcal{L}\left[te^{j{\omega}t}\right]-\displaystyle\mathcal{L}\left[te^{-j{\omega}t}\right]\right)\\
\\
&=&\frac{1}{2j}\left\{\frac{1}{(s-j{\omega})^2}-\frac{1}{(s+j{\omega})^2}\right\}\\
\\
&=&\frac{1}{2j}\left\{\frac{(s+j{\omega})^2-(s-j{\omega})^2}{(s-j{\omega})^2(s+j{\omega})^2}\right\}\\
\\
&=&\frac{1}{2j}\left\{\frac{4j{\omega}s}{(s^2+{\omega}^2)^2}\right\}\\
\\
&=&\frac{2{\omega}s}{(s^2+{\omega}^2)^2}\tag{16-8}
\end{eqnarray}

「\(t{\cos}{\omega}t\)」のラプラス変換

「\(f(t)=t{\cos}{\omega}t\)」のラプラス変換\(F(s)\)を次式に示します。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[t{\cos}{\omega}t\right]=\frac{s^2-{\omega}^2}{(s^2+{\omega}^2)^2}\tag{17-1}
\end{eqnarray}

証明方法

まず、「\({\cos}{\omega}t\)」を「\(e^■\)」の形に変形させます。

オイラーの公式より次式が成り立ちます。

\begin{eqnarray}
e^{j{\omega}t}&=&{\cos}{\omega}t+j{\sin}{\omega}t\tag{17-2}\\
\\
e^{-j{\omega}t}&=&{\cos}{\omega}t-j{\sin}{\omega}t\tag{17-3}
\end{eqnarray}

(17-2)式と(17-3)式を用いると、「\({\cos}{\omega}t=\displaystyle\frac{1}{2}(e^{j{\omega}t}+e^{-j{\omega}t})\)」が成り立ちます。

したがって、「\(f(t)=t{\cos}{\omega}t\)」は次式のように変形することができます。

\begin{eqnarray}
f(t)=t{\cos}{\omega}t=t{\;}{\cdot}{\;}\frac{1}{2}(e^{j{\omega}t}+e^{-j{\omega}t})\tag{17-4}
\end{eqnarray}

以上より、ラプラス変換の定義式に「\(f(t)=t{\cos}{\omega}t\)」を代入すると、

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&{\displaystyle\int}_0^{\infty}f(t){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}t{\cos}{\omega}t{\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}t{\;}{\cdot}{\;}\frac{1}{2}(e^{j{\omega}t}+e^{-j{\omega}t}){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&\frac{1}{2}\left({\displaystyle\int}_0^{\infty}te^{j{\omega}t}{\;}{\cdot}{\;}e^{-st}dt+{\displaystyle\int}_0^{\infty}te^{-j{\omega}t}{\;}{\cdot}{\;}e^{-st}dt\right)
\\
&=&\frac{1}{2}\left(\displaystyle\mathcal{L}\left[te^{j{\omega}t}\right]+\displaystyle\mathcal{L}\left[te^{-j{\omega}t}\right]\right)\tag{17-5}
\end{eqnarray}

のように変形することができます。

ここで、(8-1)式より、「\(\displaystyle\mathcal{L}\left[te^{-at}\right]=\displaystyle\frac{1}{(s+a)^2}\)」なので、\(\displaystyle\mathcal{L}\left[te^{j{\omega}t}\right]\)と\(\displaystyle\mathcal{L}\left[te^{-j{\omega}t}\right]\)は次式で表されます。

\begin{eqnarray}
\displaystyle\mathcal{L}\left[te^{j{\omega}t}\right]&=&\frac{1}{(s-j{\omega})^2}\tag{17-6}\\
\\
\displaystyle\mathcal{L}\left[te^{-j{\omega}t}\right]&=&\frac{1}{(s+j{\omega})^2}\tag{17-7}
\end{eqnarray}

(17-6)式と(17-7)式を(17-5)式に代入すると、次式のようになり、「\(f(t)=t{\cos}{\omega}t\)」のラプラス変換\(F(s)\)を導出することができます。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&\frac{1}{2}\left(\displaystyle\mathcal{L}\left[te^{j{\omega}t}\right]+\displaystyle\mathcal{L}\left[te^{-j{\omega}t}\right]\right)\\
\\
&=&\frac{1}{2}\left\{\frac{1}{(s-j{\omega})^2}+\frac{1}{(s+j{\omega})^2}\right\}\\
\\
&=&\frac{1}{2}\left\{\frac{(s+j{\omega})^2+(s-j{\omega})^2}{(s-j{\omega})^2(s+j{\omega})^2}\right\}\\
\\
&=&\frac{1}{2}\left\{\frac{2s^2-2{\omega}^2}{(s^2+{\omega}^2)^2}\right\}\\
\\
&=&\frac{s^2-{\omega}^2}{(s^2+{\omega}^2)^2}\tag{17-8}
\end{eqnarray}

「\({\sin}^2{\omega}t\)」のラプラス変換

「\(f(t)={\sin}^2{\omega}t\)」のラプラス変換\(F(s)\)を次式に示します。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[{\sin}^2{\omega}t\right]=\frac{2{\omega}^2}{s(s^2+4{\omega}^2)}\tag{18-1}
\end{eqnarray}

証明方法

「\(f(t)={\sin}^2{\omega}t\)」は次式のように変形することができます。

\begin{eqnarray}
f(t)={\sin}^2{\omega}t=\frac{1-{\cos}2{\omega}t}{2}\tag{18-2}
\end{eqnarray}

ラプラス変換の定義式に「\(f(t)={\sin}^2{\omega}t\)」を代入すると、

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&{\displaystyle\int}_0^{\infty}f(t){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}{\sin}^2{\omega}t{\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}\frac{1-{\cos}2{\omega}t}{2}{\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&\frac{1}{2}\left({\displaystyle\int}_0^{\infty}1{\;}{\cdot}{\;}e^{-st}dt-{\displaystyle\int}_0^{\infty}{\cos}2{\omega}t{\;}{\cdot}{\;}e^{-st}dt\right)
\\
&=&\frac{1}{2}\left(\displaystyle\mathcal{L}\left[1\right]-\displaystyle\mathcal{L}\left[{\cos}2{\omega}t\right]\right)\tag{18-3}
\end{eqnarray}

のように変形することができます。

ここで、(1-1)式より、\(\displaystyle\mathcal{L}\left[1\right]\)は次式で表されます。

\begin{eqnarray}
\displaystyle\mathcal{L}\left[1\right]=\frac{1}{s}\tag{18-4}
\end{eqnarray}

また、(11-1)式より、「\(\displaystyle\mathcal{L}\left[{\cos}{\omega}t\right]=\displaystyle\frac{s}{s^2+{\omega}^2}\)」なので、\(\displaystyle\mathcal{L}\left[{\cos}2{\omega}t\right]\)は次式で表されます。

\begin{eqnarray}
\displaystyle\mathcal{L}\left[{\cos}2{\omega}t\right]&=&\frac{s}{s^2+(2{\omega})^2}=\frac{s}{s^2+4{\omega}^2}\tag{18-5}
\end{eqnarray}

(18-4)式と(18-5)式を(18-3)式に代入すると、次式のようになり、「\(f(t)={\sin}^2{\omega}t\)」のラプラス変換\(F(s)\)を導出することができます。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&\frac{1}{2}\left(\displaystyle\mathcal{L}\left[1\right]-\displaystyle\mathcal{L}\left[{\cos}2{\omega}t\right]\right)\\
\\
&=&\frac{1}{2}\left(\frac{1}{s}-\frac{s}{s^2+4{\omega}^2}\right)\\
\\
&=&\frac{1}{2}\left\{\frac{s^2+4{\omega}^2-s^2}{s(s^2+4{\omega}^2)}\right\}\\
\\
&=&\frac{2{\omega}^2}{s(s^2+4{\omega}^2)}\tag{18-6}
\end{eqnarray}

「\({\cos}^2{\omega}t\)」のラプラス変換

「\(f(t)={\cos}^2{\omega}t\)」のラプラス変換\(F(s)\)を次式に示します。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[{\cos}^2{\omega}t\right]=\frac{s^2+2{\omega}^2}{s(s^2+4{\omega}^2)}\tag{19-1}
\end{eqnarray}

証明方法

「\(f(t)={\cos}^2{\omega}t\)」は次式のように変形することができます。

\begin{eqnarray}
f(t)={\cos}^2{\omega}t=\frac{1+{\cos}2{\omega}t}{2}\tag{19-2}
\end{eqnarray}

ラプラス変換の定義式に「\(f(t)={\cos}^2{\omega}t\)」を代入すると、

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&{\displaystyle\int}_0^{\infty}f(t){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}{\cos}^2{\omega}t{\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}\frac{1+{\cos}2{\omega}t}{2}{\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&\frac{1}{2}\left({\displaystyle\int}_0^{\infty}1{\;}{\cdot}{\;}e^{-st}dt+{\displaystyle\int}_0^{\infty}{\cos}2{\omega}t{\;}{\cdot}{\;}e^{-st}dt\right)
\\
&=&\frac{1}{2}\left(\displaystyle\mathcal{L}\left[1\right]+\displaystyle\mathcal{L}\left[{\cos}2{\omega}t\right]\right)\tag{19-3}
\end{eqnarray}

のように変形することができます。

ここで、(1-1)式より、\(\displaystyle\mathcal{L}\left[1\right]\)は次式で表されます。

\begin{eqnarray}
\displaystyle\mathcal{L}\left[1\right]=\frac{1}{s}\tag{19-4}
\end{eqnarray}

また、(11-1)式より、「\(\displaystyle\mathcal{L}\left[{\cos}{\omega}t\right]=\displaystyle\frac{s}{s^2+{\omega}^2}\)」なので、\(\displaystyle\mathcal{L}\left[{\cos}2{\omega}t\right]\)は次式で表されます。

\begin{eqnarray}
\displaystyle\mathcal{L}\left[{\cos}2{\omega}t\right]&=&\frac{s}{s^2+(2{\omega})^2}=\frac{s}{s^2+4{\omega}^2}\tag{19-5}
\end{eqnarray}

(19-4)式と(19-5)式を(19-3)式に代入すると、次式のようになり、「\(f(t)={\cos}^2{\omega}t\)」のラプラス変換\(F(s)\)を導出することができます。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&\frac{1}{2}\left(\displaystyle\mathcal{L}\left[1\right]+\displaystyle\mathcal{L}\left[{\cos}2{\omega}t\right]\right)\\
\\
&=&\frac{1}{2}\left(\frac{1}{s}+\frac{s}{s^2+4{\omega}^2}\right)\\
\\
&=&\frac{1}{2}\left\{\frac{s^2+4{\omega}^2+s^2}{s(s^2+4{\omega}^2)}\right\}\\
\\
&=&\frac{s^2+2{\omega}^2}{s(s^2+4{\omega}^2)}\tag{19-6}
\end{eqnarray}

「\({\sinh}{\omega}t\)」のラプラス変換

「\(f(t)={\sinh}{\omega}t\)」のラプラス変換\(F(s)\)を次式に示します。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[{\sinh}{\omega}t\right]=\frac{{\omega}}{s^2-{\omega}^2}\tag{20-1}
\end{eqnarray}

証明方法

「\(f(t)={\sinh}{\omega}t\)」は次式のように変形することができます。

\begin{eqnarray}
f(t)={\sinh}{\omega}t=\frac{1}{2}(e^{{\omega}t}-e^{-{\omega}t})\tag{20-2}
\end{eqnarray}

以上より、ラプラス変換の定義式に「\(f(t)={\sinh}{\omega}t\)」を代入すると、

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&{\displaystyle\int}_0^{\infty}f(t){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}{\sinh}{\omega}t{\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}\frac{1}{2}(e^{{\omega}t}-e^{-{\omega}t}){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&\frac{1}{2}\left({\displaystyle\int}_0^{\infty}e^{{\omega}t}{\;}{\cdot}{\;}e^{-st}dt-{\displaystyle\int}_0^{\infty}e^{-{\omega}t}{\;}{\cdot}{\;}e^{-st}dt\right)
\\
&=&\frac{1}{2}\left(\displaystyle\mathcal{L}\left[e^{{\omega}t}\right]-\displaystyle\mathcal{L}\left[e^{-{\omega}t}\right]\right)\tag{20-3}
\end{eqnarray}

のように変形することができます。

ここで、(7-1)式より、「\(\displaystyle\mathcal{L}\left[e^{-at}\right]=\displaystyle\frac{1}{s+a}\)」なので、\(\displaystyle\mathcal{L}\left[e^{{\omega}t}\right]\)と\(\displaystyle\mathcal{L}\left[e^{-{\omega}t}\right]\)は次式で表されます。

\begin{eqnarray}
\displaystyle\mathcal{L}\left[e^{{\omega}t}\right]&=&\frac{1}{s-{\omega}}\tag{20-4}\\
\\
\displaystyle\mathcal{L}\left[e^{-{\omega}t}\right]&=&\frac{1}{s+{\omega}}\tag{20-5}
\end{eqnarray}

(20-4)式と(20-5)式を(20-3)式に代入すると、次式のようになり、「\(f(t)={\sinh}{\omega}t\)」のラプラス変換\(F(s)\)を導出することができます。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&\frac{1}{2}\left(\displaystyle\mathcal{L}\left[e^{{\omega}t}\right]-\displaystyle\mathcal{L}\left[e^{-{\omega}t}\right]\right)\\
\\
&=&\frac{1}{2}\left(\frac{1}{s-{\omega}}-\frac{1}{s+{\omega}}\right)\\
\\
&=&\frac{1}{2}\left(\frac{s+{\omega}}{s^2-{\omega}^2}-\frac{s-{\omega}}{s^2-{\omega}^2}\right)\\
\\
&=&\frac{{\omega}}{s^2-{\omega}^2}\tag{20-6}
\end{eqnarray}

「\({\cosh}{\omega}t\)」のラプラス変換

「\(f(t)={\cosh}{\omega}t\)」のラプラス変換\(F(s)\)を次式に示します。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]=\displaystyle\mathcal{L}\left[{\cosh}{\omega}t\right]=\frac{s}{s^2-{\omega}^2}\tag{21-1}
\end{eqnarray}

証明方法

「\(f(t)={\cosh}{\omega}t\)」は次式のように変形することができます。

\begin{eqnarray}
f(t)={\cosh}{\omega}t=\frac{1}{2}(e^{{\omega}t}+e^{-{\omega}t})\tag{21-2}
\end{eqnarray}

以上より、ラプラス変換の定義式に「\(f(t)={\cosh}{\omega}t\)」を代入すると、

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&{\displaystyle\int}_0^{\infty}f(t){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}{\cosh}{\omega}t{\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&{\displaystyle\int}_0^{\infty}\frac{1}{2}(e^{{\omega}t}+e^{-{\omega}t}){\;}{\cdot}{\;}e^{-st}dt\\
\\
&=&\frac{1}{2}\left({\displaystyle\int}_0^{\infty}e^{{\omega}t}{\;}{\cdot}{\;}e^{-st}dt+{\displaystyle\int}_0^{\infty}e^{-{\omega}t}{\;}{\cdot}{\;}e^{-st}dt\right)
\\
&=&\frac{1}{2}\left(\displaystyle\mathcal{L}\left[e^{{\omega}t}\right]+\displaystyle\mathcal{L}\left[e^{-{\omega}t}\right]\right)\tag{21-3}
\end{eqnarray}

のように変形することができます。

ここで、(7-1)式より、「\(\displaystyle\mathcal{L}\left[e^{-at}\right]=\displaystyle\frac{1}{s+a}\)」なので、\(\displaystyle\mathcal{L}\left[e^{{\omega}t}\right]\)と\(\displaystyle\mathcal{L}\left[e^{-{\omega}t}\right]\)は次式で表されます。

\begin{eqnarray}
\displaystyle\mathcal{L}\left[e^{{\omega}t}\right]&=&\frac{1}{s-{\omega}}\tag{21-4}\\
\\
\displaystyle\mathcal{L}\left[e^{-{\omega}t}\right]&=&\frac{1}{s+{\omega}}\tag{21-5}
\end{eqnarray}

(21-4)式と(21-5)式を(21-3)式に代入すると、次式のようになり、「\(f(t)={\cosh}{\omega}t\)」のラプラス変換\(F(s)\)を導出することができます。

\begin{eqnarray}
F(s)=\displaystyle\mathcal{L}\left[f(t)\right]&=&\frac{1}{2}\left(\displaystyle\mathcal{L}\left[e^{{\omega}t}\right]+\displaystyle\mathcal{L}\left[e^{-{\omega}t}\right]\right)\\
\\
&=&\frac{1}{2}\left(\frac{1}{s-{\omega}}+\frac{1}{s+{\omega}}\right)\\
\\
&=&\frac{1}{2}\left(\frac{s+{\omega}}{s^2-{\omega}^2}+\frac{s-{\omega}}{s^2-{\omega}^2}\right)\\
\\
&=&\frac{s}{s^2-{\omega}^2}\tag{21-6}
\end{eqnarray}

まとめ

この記事では『ラプラス変換』について、以下の内容を説明しました。

• ラプラス変換の「一覧表・変換表」
• ラプラス変換の「一覧表・変換表」の証明方法

お読み頂きありがとうございました。

当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。

全記事一覧

また、記事下に当サイトの人気記事を記載しています。ご参考になれば幸いです。