トランスの漏れインダクタンスとは？計算・測定方法などを解説！

この記事ではトランスの『漏れインダクタンス』について

トランスの『漏れインダクタンス』とは？
トランスの『漏れインダクタンス』と『等価回路』
トランスの『漏れインダクタンス』の測定と計算方法

などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。

トランスの『漏れインダクタンス』とは？

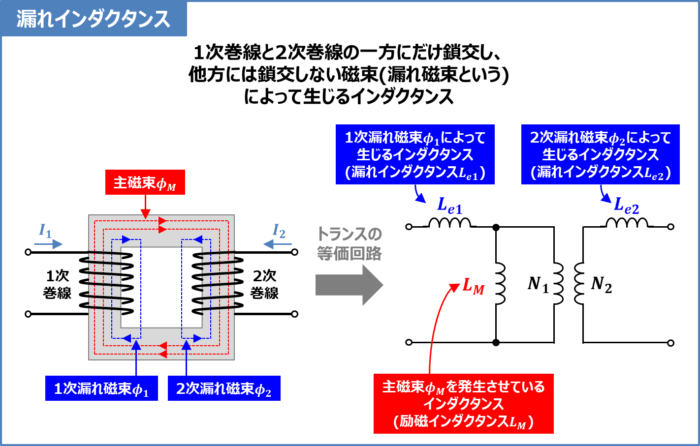
トランスの漏れインダクタンスは「1次巻線と2次巻線の一方にだけ鎖交し、他方には鎖交しない磁束(漏れ磁束という)」によって生じるインダクタンスです。

上記について、もう少し詳しく説明します。

上図にトランスから発生する磁束を示しています。トランスから発生する磁束を分類すると、主磁束(\({\phi}_M)\)と漏れ磁束\(({\phi}_1\)または\({\phi}_2)\)に分けられます。

主磁束は、1次巻線と2次巻線の双方と鎖交する磁束です。トランスの磁束には、主磁束の他に「1次巻線だけと鎖交し、2次巻線とは鎖交しない1次漏れ磁束\({\phi}_1\)」と「2次巻線とだけ鎖交し、1次巻線とは鎖交しない2次漏れ磁束\({\phi}_2\)」があります。

主磁束を発生させているインダクタンスが励磁インダクタンス\(L_M\)となります。一次側漏れ磁束\({\phi}_1\)によって生じるインダクタンスが1次漏れインダクタンス\(L_{e1}\)、2次側漏れ磁束\({\phi}_2\)によって生じるインダクタンスが2次漏れインダクタンス\(L_{e2}\)となります。

補足

漏れインダクタンスは「漏洩インダクタンス」や「リーケージインダクタンス」とも呼ばれています。
漏れインダクタンスは英語では「Leakage Inductance」と書きます。
主磁束は英語では「Main Flux」と書きます。
漏れ磁束は英語では「Leakage Flux」と書きます。
理想的なトランスの場合、主磁束のみしかありませんが、実際のトランスには磁気漏れがあるので、必ず漏れ磁束があります。この漏れ磁束は1次巻線または2次巻線のみしか鎖交しないため、変圧作用には寄与しません。

トランスの『漏れインダクタンス』と『等価回路』

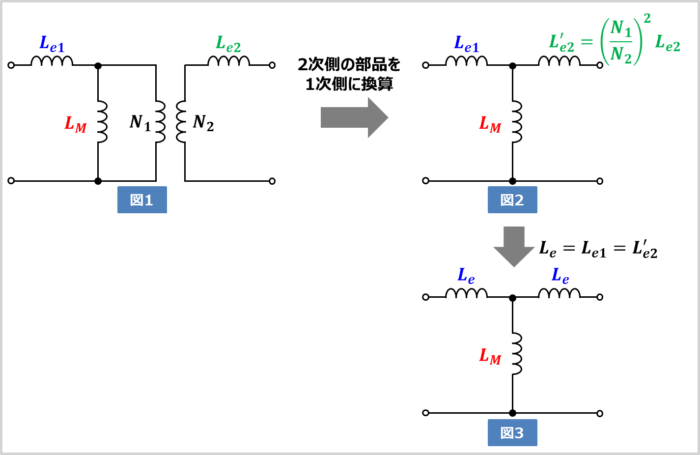
図1に示す等価回路において、2次側の部品を1次側に換算させると、図2のようになります。

1次巻線の巻数を\(N_1\)、2次巻線の巻数を\(N_2\)とすると、「2次漏れインダクタンス\(L_{e2}\)を1次側に換算した時のインダクタンス\({L_{e2}}'\)」は次式で表されます。

\begin{eqnarray}
{L_{e2}}'=\left(\frac{N_1}{N_2}\right)^2L_{e2}\tag{1}
\end{eqnarray}

また、「1次漏れインダクタンス\(L_{e1}\)」と「2次漏れインダクタンス\(L_{e2}\)を1次側に換算した時のインダクタンス\({L_{e2}}'\)」が等しいと仮定し、これを「漏れインダクタンス\(L_e\)」と置くと、次式で表すことができます。

\begin{eqnarray}
L_e=L_{e1}={L_{e2}}'\tag{2}
\end{eqnarray}

以上より、トランスは「励磁インダクタンス\(L_M\)」と「漏れインダクタンス\(L_e\)」のみの等価回路(図3)に変換することができます。

補足

図1～3に示す等価回路では、1次巻線や2次巻線の巻線抵抗、浮遊容量、鉄損抵抗などは省略しています。

トランスの『漏れインダクタンス』の測定と計算方法

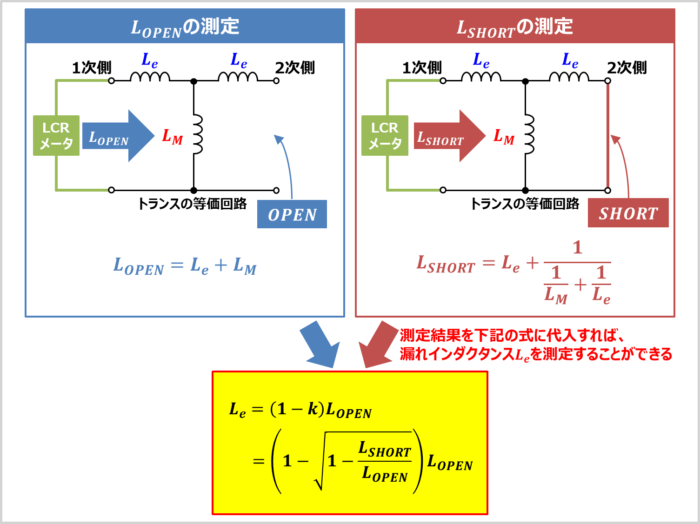
先ほど示した図3の等価回路を用いて、トランスの漏れインダクタンス\(L_e\)の「測定」と「計算方法」について説明します。

2次側を開放し、1次側のインダクタンスをLCRメータ等の測定器で測定します。2次側を開放した時の1次側のインダクタンスを\(L_{OPEN}\)とすると、\(L_{OPEN}\)は次式で表されます。なお、この方法で測定したインダクタンス\(L_{OPEN}\)は自己インダクタンスと呼ばれています。

\begin{eqnarray}
L_{OPEN}=L_e+L_M\tag{3}
\end{eqnarray}

2次側を短絡し、1次側のインダクタンスを測定します。2次側を短絡させた時の1次側のインダクタンスを\(L_{SHORT}\)とすると、\(L_{SHORT}\)は次式で表されます。

\begin{eqnarray}
L_{SHORT}=L_e+\frac{1}{\displaystyle\frac{1}{L_M}+\displaystyle\frac{1}{L_e}}\tag{4}
\end{eqnarray}

また、結合係数\(k\)は\(L_{OPEN}\)は\(L_{SHORT}\)を用いると、次式で表されます。

\begin{eqnarray}
k=\sqrt{1-\displaystyle\frac{L_{SHORT}}{L_{OPEN}}}\tag{5}
\end{eqnarray}

励磁インダクタンス\(L_M\)は結合係数\(k\)と\(L_{OPEN}\)を用いると、次式で表されます。

\begin{eqnarray}
L_M=kL_{OPEN}\tag{6}
\end{eqnarray}

(6)式を(3)式に代入すると、漏れインダクタンス\(L_e\)は次式で表されます。

\begin{eqnarray}
L_{OPEN}&=&L_e+L_M\\
\\
&=&L_e+kL_{OPEN}\\
\\
{\Leftrightarrow}L_e&=&(1-k)L_{OPEN}\\
\\
&=&\left(1-\sqrt{1-\displaystyle\frac{L_{SHORT}}{L_{OPEN}}}\right)L_{OPEN}\tag{7}
\end{eqnarray}

「2次側を開放した時の1次側のインダクタンス\(L_{OPEN}\)」と「2次側を短絡した時の1次側のインダクタンス\(L_{SHORT}\)」を測定し、(7)式に代入すれば、漏れインダクタンス\(L_e\)を測定することができます。

近似でLeを求める方法

通常のトランスは漏れインダクタンス\(L_e\)が非常に小さく、「\(L_M{\;}{\gg}{\;}L_e\)」とみなせるので、(3)式を

\begin{eqnarray}
L_{OPEN}=L_e+L_M{\;}{\approx}{\;}L_M\tag{8}
\end{eqnarray}

と近似し、「2次側を開放した時の1次側のインダクタンス\(L_{OPEN}\)」を「励磁インダクタンス\(L_M\)」と考えている資料もあります。

また同様に、「\(L_M{\;}{\gg}{\;}L_e\)」とみなして、(4)式を

\begin{eqnarray}
L_{SHORT}&=&L_e+\frac{1}{\displaystyle\frac{1}{L_M}+\displaystyle\frac{1}{L_e}}\\
\\
&=&L_e+\frac{L_e}{\displaystyle\frac{L_e}{L_M}+\displaystyle\frac{L_e}{L_e}}\\
\\
&{\approx}&L_e+\frac{L_e}{0+1}\\
\\
&{\approx}&2L_e\\
\\
{\Leftrightarrow}L_e&{\approx}&\frac{L_{SHORT}}{2}\tag{9}
\end{eqnarray}

と近似し、「2次側を短絡した時の1次側のインダクタンス\(L_{SHORT}\)」の半分(1/2)を「漏れインダクタンス\(L_e\)」と考えている資料もあります。

漏れインダクタンス\(L_e\)が非常に小さいトランスには(8)式と(9)式の近似が有効です。

【補足】電気学会と工業会による漏れインダクタンスの定義

「電気学会」と「トランス工業会」では漏れインダクタンスの定義が異なります。今まで説明したのは電気学会による漏れインダクタンス\(L_e\)となります。

「電気学会」や「電磁気学」などの書籍では、漏れインダクタンス\(L_e\)は「1次巻線と2次巻線の一方にだけ鎖交し、他方には鎖交しない磁束(漏れ磁束という)」によって生じるインダクタンスと定義しています。

一方、「トランス工業会」や「JIS C6435」では2次側を短絡した時の1次側のインダクタンス(短絡インダクタンス)\(L_{SHORT}\)を漏れインダクタンスとしています。なお、短絡インダクタンスは英語では「Short-Circuit inductance」と書くため、工業会で定めた漏れインダクタンス(短絡インダクタンス)の記号には英語の略を用いて、\(L_{SC}\)を用いることが多いです。

「工業会で定めた漏れインダクタンス(短絡インダクタンス)\(L_{SC}\)」は(5)式を用いると次式で表されます。

\begin{eqnarray}
k&=&\sqrt{1-\displaystyle\frac{L_{SHORT}}{L_{OPEN}}}\\
\\
&=&\sqrt{1-\displaystyle\frac{L_{SC}}{L_{OPEN}}}\\
\\
{\Leftrightarrow}k^2&=&1-\displaystyle\frac{L_{SC}}{L_{OPEN}}\\
\\
{\Leftrightarrow}L_{SC}&=&(1-k^2)L_{OPEN}\tag{10}
\end{eqnarray}

また、「2次側を開放した時の1次側のインダクタンス\(L_{OPEN}\)」は(7)式を用いると次式で表されます。

\begin{eqnarray}
L_{OPEN}=\frac{1}{1-k}L_e\tag{11}
\end{eqnarray}

(10)式と(11)式を用いると、「漏れインダクタンス\(L_e\)」と「工業会で定めた漏れインダクタンス(短絡インダクタンス)\(L_{SC}\)」の関係式は次式となります。

\begin{eqnarray}
L_{SC}&=&(1-k^2)L_{OPEN}\\
\\
&=&(1-k^2)\frac{1}{1-k}L_e\\
\\
&=&(1+k)(1-k)\frac{1}{1-k}L_e\\
\\
&=&(1+k)L_e\tag{12}
\end{eqnarray}