この記事では『インダクタの並列接続』について
- 並列接続されたインダクタの合成インダクタンスの『計算方法』・『証明』・『例題』
などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。
【インダクタの並列接続】インダクタンスの『計算』
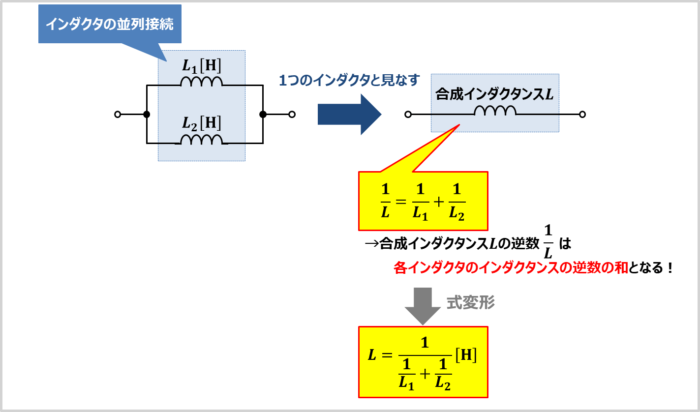
インダクタ\(L_1\)とインダクタ\(L_2\)を並列に接続することを「インダクタの並列接続」といいます。
「インダクタンスが\(L_1{\mathrm{[H]}}\)のインダクタ」と「インダクタンスが\(L_2{\mathrm{[H]}}\)のインダクタ」が並列接続されている時、合成インダクタンス\(L\)の逆数\(\displaystyle\frac{1}{L}\)は各インダクタのインダクタンスの逆数の和で計算することができ、次式で表されます。
\begin{eqnarray}
\frac{1}{L}=\frac{1}{L_1}+\frac{1}{L_2}\tag{1}
\end{eqnarray}
したがって、(1)式を変形すると、合成インダクタンス\(L\)は次式で表されます。
\begin{eqnarray}
L=\frac{1}{\displaystyle\frac{1}{L_1}+\displaystyle\frac{1}{L_2}}=\frac{L_1×L_2}{L_1+L_2}{\mathrm{[H]}}\tag{2}
\end{eqnarray}
「並列接続」と「和分の積」
並列接続されている2つのインダクタの合成インダクタンスを求める時、次式で示すような「和分の積」で求めることができます。
\begin{eqnarray}
L=\frac{\mbox{2つのインダクタンスの積(かけ算)}}{\mbox{2つのインダクタンスの和(足し算)}}=\frac{L_1×L_2}{L_1+L_2}{\mathrm{[H]}}\tag{3}
\end{eqnarray}
(3)式は分母が和、分子が積になっているので、和分の積と呼ばれています。
ただし、注意があります。
「和分の積が使えるのは、2つのインダクタが並列接続されている時のみ!」です。
「3つ以上のインダクタが並列接続されている時」には「和分の積」は使えません。
合成インダクタンスとは
複数のインダクタをまとめて1つのインダクタとした時のインダクタンスを合成インダクタンスと呼びます。
Nつのインダクタが並列接続されている時
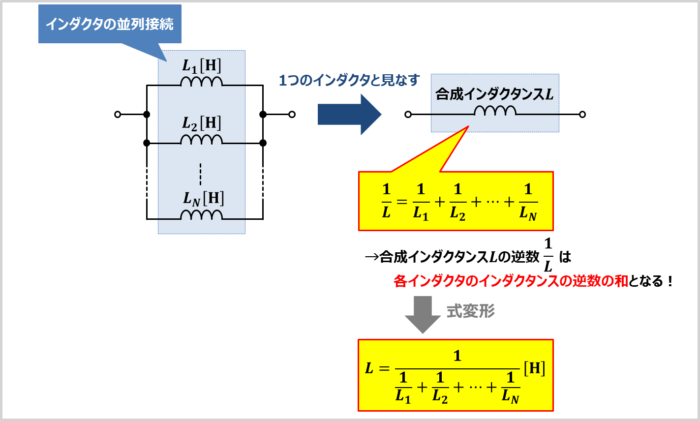
(1)式はインダクタが3つ以上並列接続されている時にも成り立ちます。
上図に示しているのは、Nつのインダクタ(各インダクタのインダクタンスを\(L_1{\mathrm{[H]}}\),\(L_2{\mathrm{[H]}}\),・・・,\(L_N{\mathrm{[H]}}\)とする)が並列接続されている回路です。
この回路においても、合成インダクタンス\(L\)の逆数\(\displaystyle\frac{1}{L}\)は各インダクタのインダクタンスの逆数の和で計算することができ、次式で表されます。
\begin{eqnarray}
\frac{1}{L}=\frac{1}{L_1}+\frac{1}{L_2}+{\cdots}+\frac{1}{L_N}\tag{4}
\end{eqnarray}
したがって、(4)式を変形すると、合成インダクタンス\(L\)は次式で表されます。
\begin{eqnarray}
L=\frac{1}{\displaystyle\frac{1}{L_1}+\displaystyle\frac{1}{L_2}+{\cdots}+\displaystyle\frac{1}{L_N}}{\mathrm{[H]}}\tag{5}
\end{eqnarray}
例えば、3つのインダクタ(各インダクタのインダクタンスを\(L_1{\mathrm{[H]}}\),\(L_2{\mathrm{[H]}}\),\(L_3{\mathrm{[H]}}\)とする)が並列接続されている時の合成インダクタンス\(L\)は次式となります。
\begin{eqnarray}
L=\frac{1}{\displaystyle\frac{1}{L_1}+\displaystyle\frac{1}{L_2}+\displaystyle\frac{1}{L_3}}{\mathrm{[H]}}\tag{6}
\end{eqnarray}
注意点
3つのインダクタが並列接続されている時に「和分の積」を用いて、合成インダクタンス\(L\)を
\begin{eqnarray}
C=\frac{\mbox{3つのインダクタンスの積(かけ算)}}{\mbox{3つのインダクタンスの和(足し算)}}=\frac{L_1×L_2×L_3}{L_1+L_2+L_3}{\mathrm{[H]}}\tag{7}
\end{eqnarray}
としないように気を付けてください。繰り返しになりますが、和分の積が使えるのは「2つのインダクタが並列接続されている時のみ!」です。
【インダクタの並列接続】インダクタンスの『証明』
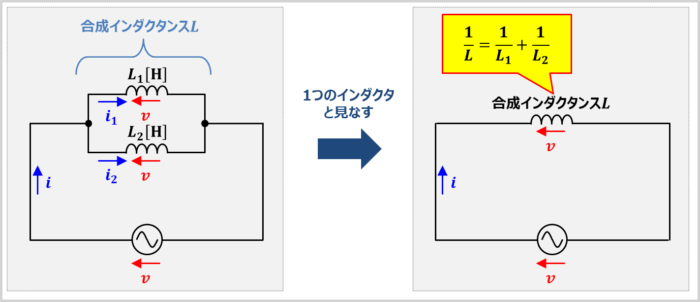
上図に示すように、「\(L_1{\mathrm{[H]}}\)のインダクタ」と「\(L_2{\mathrm{[H]}}\)のインダクタ」を並列接続した後、電源電圧\(v{\mathrm{[V]}}\)を印加します。
この時、「インダクタ\(L_1\)に流れる電流\(i_1\)」と「インダクタ\(L_2\)に流れる電流\(i_2\)」は次式で表されます。
\begin{eqnarray}
i_1&=&\frac{1}{L_1}{\displaystyle\int}v{\;}dt\tag{8}\\
\\
i_2&=&\frac{1}{L_2}{\displaystyle\int}v{\;}dt\tag{9}
\end{eqnarray}
また、並列回路に流れる電流\(i{\mathrm{[A]}}\)は各インダクタに流れる電流の和となるので、次式が成り立ちます。
\begin{eqnarray}
i=i_1+i_2\tag{10}
\end{eqnarray}
ここで、2つのインダクタ(\(L_1{\mathrm{[H]}}\)と\(L_2{\mathrm{[H]}}\))をまとめて1つのインダクタとした時のインダクタンスを\(L{\mathrm{[H]}}\)とすると、次式が成り立ちます。
\begin{eqnarray}
i=\frac{1}{L}{\displaystyle\int}v{\;}dt\tag{11}
\end{eqnarray}
(8)式と(9)式と(11)式を(10)式に代入すると、次式のようになり、合成インダクタンス\(L\)の逆数\(\displaystyle\frac{1}{L}\)は各インダクタのインダクタンスの逆数の和で計算できることが分かります。
\begin{eqnarray}
i&=&i_1+i_2\\
\\
{\Leftrightarrow}\frac{1}{L}{\displaystyle\int}v{\;}dt&=&\frac{1}{L_1}{\displaystyle\int}v{\;}dt+\frac{1}{L_2}{\displaystyle\int}v{\;}dt\\
\\
{\Leftrightarrow}\frac{1}{L}&=&\frac{1}{L_1}+\frac{1}{L_2}\tag{12}
\end{eqnarray}
【インダクタの並列接続】インダクタンスを求める例題
例題
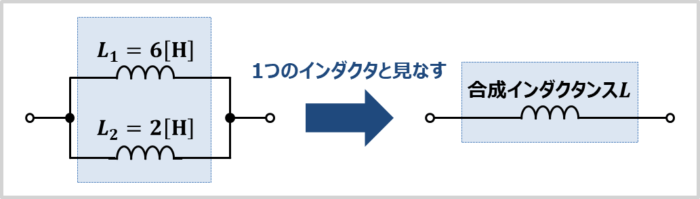
上図に示した回路において、インダクタ\(L_1\)が\(6{\mathrm{[H]}}\)、インダクタ\(L_2\)が\(2{\mathrm{[H]}}\)の時、インダクタ\(L_1\)と\(L_2\)の合成インダクタンス\(L\)は何\({\mathrm{H}}\)でしょうか。
「\(L_1=6{\mathrm{[H]}}\)」と「\(L_2=2{\mathrm{[H]}}\)」を(2)式に代入すると、インダクタ\(L_1\)と\(L_2\)の合成インダクタンス\(L\)を求めることができ、下記の値となります。
\begin{eqnarray}
L&=&\frac{1}{\displaystyle\frac{1}{L_1}+\displaystyle\frac{1}{L_2}}{\mathrm{[H]}}\\
\\
&=&\frac{1}{\displaystyle\frac{1}{6}+\displaystyle\frac{1}{2}}{\mathrm{[H]}}\\
\\
&=&1.5{\mathrm{[H]}}\tag{13}
\end{eqnarray}
まとめ
この記事では『インダクタの並列接続』について、以下の内容を説明しました。
- 並列接続されたインダクタの合成インダクタンスの『計算方法』・『証明』・『例題』
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。
また、記事下に当サイトの人気記事を記載しています。ご参考になれば幸いです。






