この記事では『ホイートストンブリッジ』について
- ホイートストンブリッジとは
- ホイートストンブリッジの『平衡条件』と『導出方法』
- ホイートストンブリッジで未知の抵抗値を求める方法
などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。
ホイートストンブリッジとは
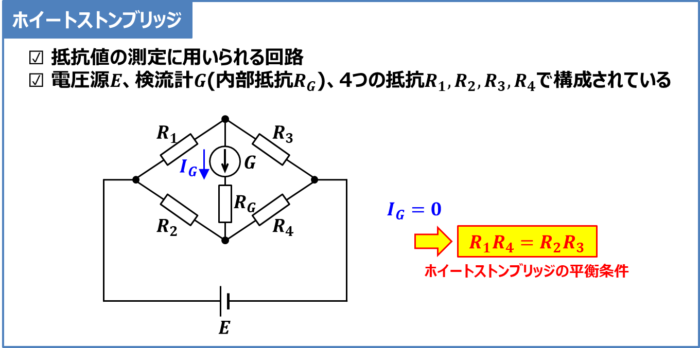
ホイートストンブリッジは、抵抗値の測定に用いられる回路です。電圧源\(E\)、検流計\(G\)(内部抵抗\(R_G\))、4つの抵抗\(R_1,R_2,R_3,R_4\)から構成されています。
「抵抗\(R_1\)と\(R_4\)を掛け算したもの(\(R_1R_4\))」と「抵抗\(R_2\)と\(R_3\)を掛け算したもの(\(R_2R_3\))」が等しくなる条件が、ホイートストンブリッジの平衡条件となります。平衡条件においては、検流計\(G\)には電流が流れません(\(I_G=0{\mathrm{[A]}}\))。
ホイートストンブリッジの平衡条件
\begin{eqnarray}
R_1R_4=R_2R_3\tag{1}
\end{eqnarray}
(1)式の平衡条件は、「向き合った抵抗(例えば、抵抗\(R_1\)と\(R_3\))の掛け算同士が等しくなる」と覚えましょう。このようなことを「たすき掛け」ということもあります(平衡条件の導出方法に関しては、次項で説明します)。
ホイートストンブリッジが平衡条件の時(検流計\(G\)に電流\(I_G\)が流れていない時)、抵抗\(R_1~R_4\)のうち、3つの抵抗値が既知であれば、残りの抵抗値は(1)式を用いて導出することができます。
補足
- 検流計\(G\)とは、非常に小さな電流が流れただけで、針が動く計器です。電流の『有無』と『向き』を計測することができます。
- ホイートストンブリッジの「ホイートストン」は「アメリカの物理学者チャールズ・ホイートストン」が由来です。ホイートストンブリッジは1833年にサミュエル・ハンター・クリスティが発明した後、1843年にチャールズ・ホイートストンによって広められ、広く使われるようになりました。
- ホイートストンブリッジの「ブリッジ」は「橋(Bridge)」が由来です。検流計\(G\)が2つの導線の間を橋のように接続されています。
- ホイートストンブリッジは英語では「Wheatstone Bridge」と書きます。
ホイートストンブリッジの平衡条件の導出方法
ホイートストンブリッジの平衡条件は次式で表されることを説明しました。
ホイートストンブリッジの平衡条件
\begin{eqnarray}
R_1R_4=R_2R_3\tag{1}
\end{eqnarray}
ではこれから、(1)式の平衡条件の導出方法について説明します。
導出方法
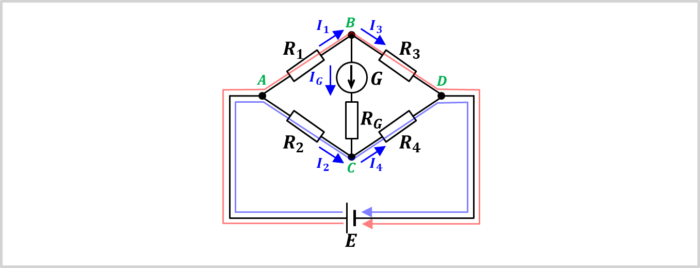
上図に示すように、\(A~D\)点、電流\(I_1~I_4\)を割り当てます。
ホイートストンブリッジが平衡条件の時、検流計\(G\)には電流が流れていません(\(I_G=0{\mathrm{[A]}}\))。そのため、「電流\(I_1\)と電流\(I_3\)」、「電流\(I_2\)と電流\(I_4\)」が等しくなるので、次式が成り立ちます。
\begin{eqnarray}
I_1&=&I_3\tag{2}\\
\\
I_2&=&I_4\tag{3}
\end{eqnarray}
ここで、赤色の電流経路と青色の電流経路に対して、キルヒホッフの第二法則を適用すると、次式が成り立ちます。
\begin{eqnarray}
E&=&R_1I_1+R_3I_1{\;}{\Leftrightarrow}{\;}I_1&=&\frac{E}{R_1+R_3}\tag{4}\\
\\
E&=&R_2I_2+R_4I_2{\;}{\Leftrightarrow}{\;}I_2&=&\frac{E}{R_2+R_4}\tag{5}
\end{eqnarray}
したがって、\(B\)点と\(C\)点の電位\(V_B\)および\(V_C\)は次式となります。
\begin{eqnarray}
V_B&=&R_3I_1=\frac{R_3}{R_1+R_3}E\tag{6}\\
\\
V_C&=&R_4I_2=\frac{R_4}{R_2+R_4}E\tag{7}
\end{eqnarray}
検流計\(G\)には電流が流れない(\(I_G=0{\mathrm{[A]}}\))ということは、電位\(V_B\)と\(V_C\)が等しいということなので次式が成り立ちます。
\begin{eqnarray}
V_B&=&V_C\\
\\
{\Leftrightarrow}\frac{R_3}{R_1+R_3}E&=&\frac{R_4}{R_2+R_4}E\\
\\
{\Leftrightarrow}R_1R_4&=&R_2R_3\tag{8}
\end{eqnarray}
上式がホイートストンブリッジの平衡条件となります。
ホイートストンブリッジで未知の抵抗値を求めてみよう
繰り返しになりますが、ホイートストンブリッジが平衡条件の時(検流計\(G\)に電流\(I_G\)が流れていない時)は次式が成り立ちます。
ホイートストンブリッジの平衡条件
\begin{eqnarray}
R_1R_4=R_2R_3\tag{1}
\end{eqnarray}
この平衡条件を利用すると、未知の抵抗値を測定することができます。
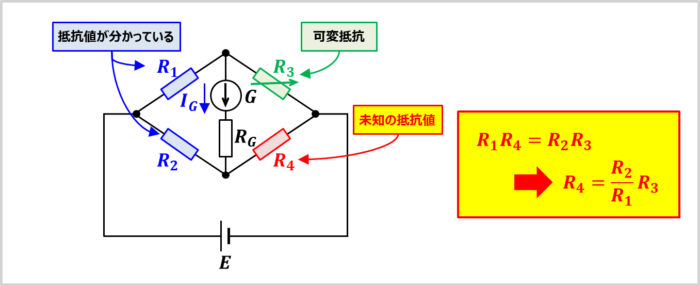
例えば、抵抗値が分かっている抵抗\(R_1\)と\(R_2\)、抵抗値を調整することができる可変抵抗\(R_3\)、未知の抵抗値の抵抗\(R_4\)から構成されているホイートストンブリッジがあるとします。
このホイートストーンブリッジにおいて、可変抵抗\(R_3\)の抵抗値を調整して、検流計\(G\)に流れる電流\(I_G\)を\(0{\mathrm{[A]}}\)にします(つまり、平衡条件にします)。
平衡条件の時は「\(R_1R_4=R_2R_3\)」が成り立つので、「\(R_4=\)」の形に変形すると、次式となります。
\begin{eqnarray}
R_4=\frac{R_2}{R_1}R_3\tag{9}
\end{eqnarray}
(9)式には電圧源\(E\)がありません。また、検流計\(G\)に流れる電流\(I_G\)は\(0{\mathrm{[A]}}\)です。そのため、ホイートストーンブリッジでは、「電圧源\(E\)」や「検流計\(G\)の内部抵抗\(R_G\)」の影響を受けずに、未知の抵抗値を測定することができます。
まとめ
この記事では『ホイートストンブリッジ』について、以下の内容を説明しました。
- ホイートストンブリッジとは
- ホイートストンブリッジの『平衡条件』と『導出方法』
- ホイートストンブリッジで未知の抵抗値を求める方法
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。
また、下記に当サイトの人気記事を記載しています。ご参考になれば幸いです。






