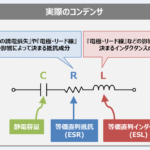
この記事ではコンデンサの『周波数特性』について
- コンデンサの『周波数特性』
- コンデンサの『周波数特性』がV字型になる理由
- 静電容量Cのみが変化した時の『周波数特性』の変化
- ESRのみが変化した時の『周波数特性』の変化
- ESLのみが変化した時の『周波数特性』の変化
などを図を用いて分かりやすく説明するように心掛けています。ご参考になれば幸いです。
コンデンサの『周波数特性』
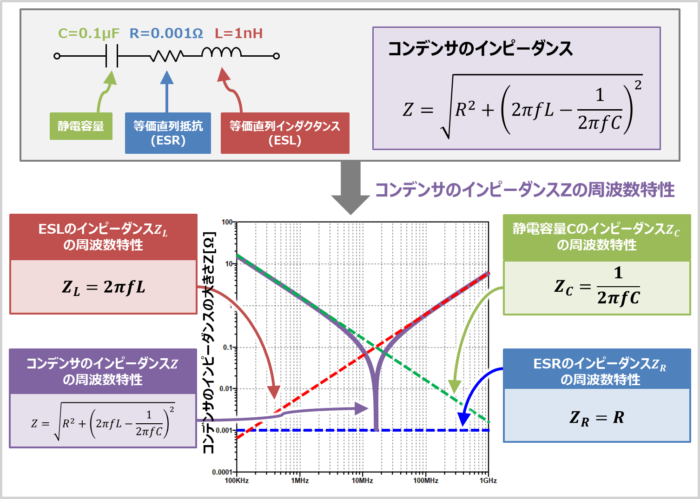
コンデンサの静電容量をC[F]、等価直列抵抗(ESR)をR[Ω]、等価直列インダクタンス(ESL)をL[H]とすると、コンデンサのインピーダンスZは次式で表されます(ω=2πf[rad/s])。
Z&=&\sqrt{R^2+\left({\omega}L-\frac{1}{{\omega}C}\right)^2}\\
\\
&=&\sqrt{R^2+\left(2{\pi}fL-\frac{1}{2{\pi}fC}\right)^2}
\end{eqnarray}
上図に示しているのは『コンデンサのインピーダンスZの周波数特性(周波数fが変化した時のインピーダンスZの変化を表す特性)』です。横軸が周波数f、縦軸がインピーダンスZとなっています。一例として、静電容量を『C=0.1μF』、ESRを『R=0.001Ω』、ESLを『L=1nH』にしています。
なお、上図において、紫色、緑色、青色、赤色の線は下記を示しています。
- 紫色の線
- 緑色の線
- 青色の線
- 赤色の線
コンデンサのインピーダンス\(Z\left(=\sqrt{R^2+\left(2{\pi}fL-\displaystyle\frac{1}{2{\pi}fC}\right)^2}\right)\)の周波数特性。
静電容量Cのみのコンデンサ(理想コンデンサ)のインピーダンス\(Z_C\left(=\displaystyle\frac{1}{2{\pi}fC}\right)\)の周波数特性。周波数が高くなると、インピーダンスZCが低下する。
等価直列抵抗(ESR)のインピーダンス\(Z_R\left(=R\right)\)の周波数特性。周波数によらず一定となる。
等価直列インダクタンス(ESL)のインピーダンス\(Z_L\left(=2{\pi}fL\right)\)の周波数特性。周波数が高くなると、インピーダンスZLが増加する。
あわせて読みたい
等価直列抵抗(ESR)と等価直列インダクタンス(ESL)について詳しく知りたい方は下記の記事で別途説明していますので、ご参考になれば幸いです。
-

『等価直列抵抗(ESR)』と『等価直列インダクタンス(ESL)』とは?【コンデンサ】
続きを見る
コンデンサの『周波数特性』がV字型になる理由
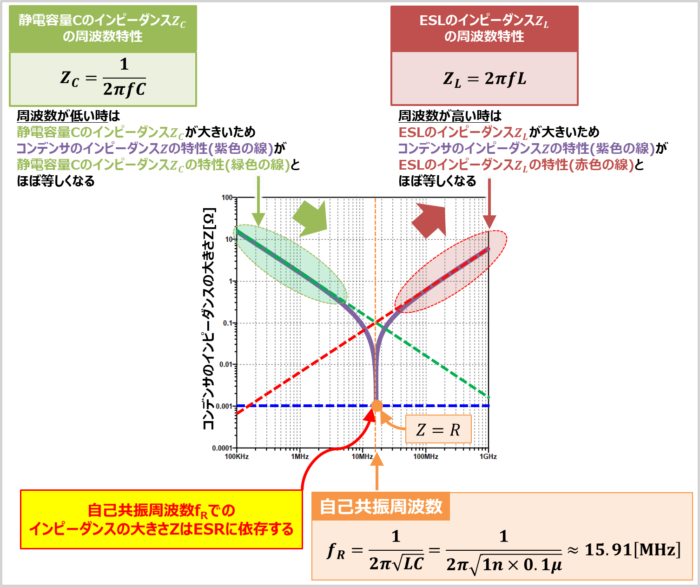

次に、周波数特性がV字型になる理由を説明します。
- 周波数が低い時
- 周波数が高い時
- 自己共振周波数
周波数が低い時は、静電容量Cのみのコンデンサ(理想コンデンサ)のインピーダンス\(Z_C\left(=\displaystyle\frac{1}{2{\pi}fC}\right)\)が大きいので、支配的となります。そのため、コンデンサのインピーダンスZの特性(紫色の線)が静電容量Cのみのコンデンサ(理想コンデンサ)のインピーダンスZCの特性(緑色の線)とほぼ等しくなります。
周波数が高い時は、等価直列インダクタンス(ESL)のインピーダンス\(Z_L\left(=2{\pi}fL\right)\)が大きいため、支配的となります。そのため、コンデンサのインピーダンスZの特性(紫色の線)がESLのインピーダンスZLの特性(赤色の線)とほぼ等しくなります。
『静電容量Cのみのコンデンサ(理想コンデンサ)のインピーダンスZC』と『等価直列インダクタンス(ESL)のインピーダンスZL』が等しくなる周波数を自己共振周波数fRといい、以下の値となります。
\begin{eqnarray}
Z_C&=&Z_L\\
\\
\frac{1}{2{\pi}f_RC}&=&2{\pi}f_RL\\
\\
{\Leftrightarrow}f_R&=&\frac{1}{2{\pi}\sqrt{LC}}\\
\\
&=&\frac{1}{2{\pi}\sqrt{1×10^{-9}×0.1×10^{-6}}}\\
\\
&{\approx}&15.91{\mathrm{[MHz]}}
\end{eqnarray}
自己共振周波数fRより低い周波数では、『静電容量Cのみのコンデンサ(理想コンデンサ)のインピーダンスZC』の方が大きいので、周波数が高くなると、インピーダンスZが低下します。
自己共振周波数fRより高い周波数では、『等価直列インダクタンス(ESL)のインピーダンスZL』の方が大きいので、周波数が高くなると、インピーダンスZが増加します。
また、自己共振周波数fRではコンデンサのインピーダンスZは以下の値となります。
\begin{eqnarray}
Z&=&\sqrt{R^2+\left(2{\pi}f_RL-\frac{1}{2{\pi}f_RC}\right)^2}\\
\\
&=&\sqrt{R^2+0^2}\\
\\
&=&R\\
\\
&=&0.001{\mathrm{[{\Omega}]}}
\end{eqnarray}
すなわち、自己共振周波数fRにおけるコンデンサのインピーダンスZはESRの大きさRに依存します。また、自己共振周波数fRでコンデンサのインピーダンスZが最小になります。
これが、コンデンサのインピーダンスZの周波数特性がV字型になる理由です。
では次に、コンデンサのインピーダンスZにおいて、
- 静電容量Cのみが変化した時の『周波数特性』の変化
- ESRのみが変化した時の『周波数特性』の変化
- ESLのみが変化した時の『周波数特性』の変化
について説明します。
補足
コンデンサをノイズ吸収用途(デカップリングコンデンサなど)で使用する場合、インピーダンスの大きさでノイズ吸収効果が決まります。そのため、以下のポイントで部品を選定する必要があります。
- ノイズの周波数とコンデンサの自己共振周波数fRが近いこと
- ESRが小さいこと
- 高周波ノイズの場合、ESLが小さいこと
『デカップリングコンデンサって何?』という方は下記の記事で説明していますので、ご参考にしてください。
-


『カップリングコンデンサ』と『デカップリングコンデンサ』の違いと特徴!
続きを見る
静電容量Cのみが変化した時の『周波数特性』の変化
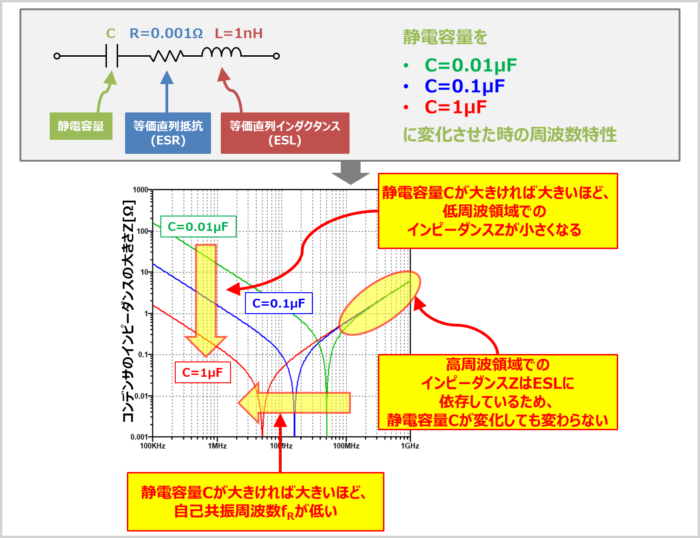

上図に静電容量Cのみが変化した時の『周波数特性』を示しています。
一例として、ESRが『R=0.001Ω』、ESLが『L=1nH』のコンデンサにおいて、静電容量Cを『C=0.01uF、0.1uF、1uF』に変化させています。
静電容量Cのみが変化した時の『周波数特性』を見ると下記のことが分かります。
- 低い周波数でのインピーダンスZは、静電容量Cが大きければ大きいほど、小さくなる。
- 高い周波数でのインピーダンスZは、ESLに依存しているため、静電容量Cが変化しても、変わらない。
- 自己共振周波数fRは静電容量Cが大きければ大きいほど、低くなる。
つまり、静電容量Cを大きくしたからといって、高い周波数でインピーダンスZが下がるわけではありません。高い周波数でインピーダンスZを下げるためには、ESLを小さくする必要があります。
ESRのみが変化した時の『周波数特性』の変化
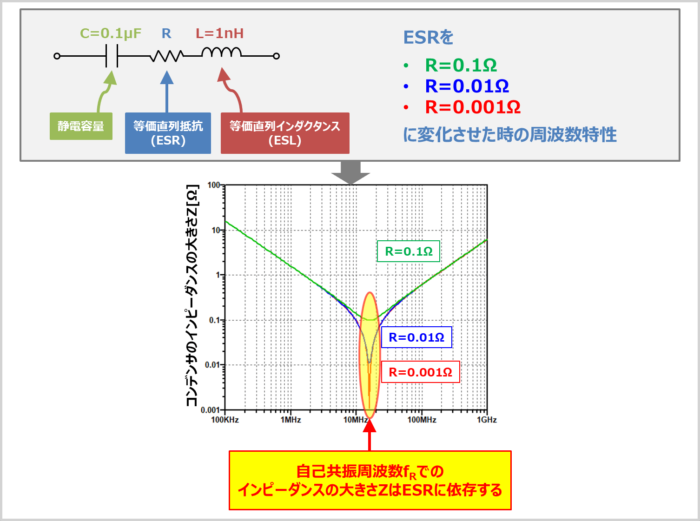

上図にESRのみが変化した時の『周波数特性』を示しています。
一例として、静電容量が『C=0.1μF』、ESLが『L=1nH』のコンデンサにおいて、ESRを『R=0.1Ω、0.01Ω、0.001Ω』に変化させています。
ESRのみが変化した時の『周波数特性』を見ると下記のことが分かります。
- 自己共振周波数fRでのインピーダンスZはESRの大きさに依存している。言い換えれば、インピーダンスZの下限はESRで決まるということ。
ESLのみが変化した時の『周波数特性』の変化
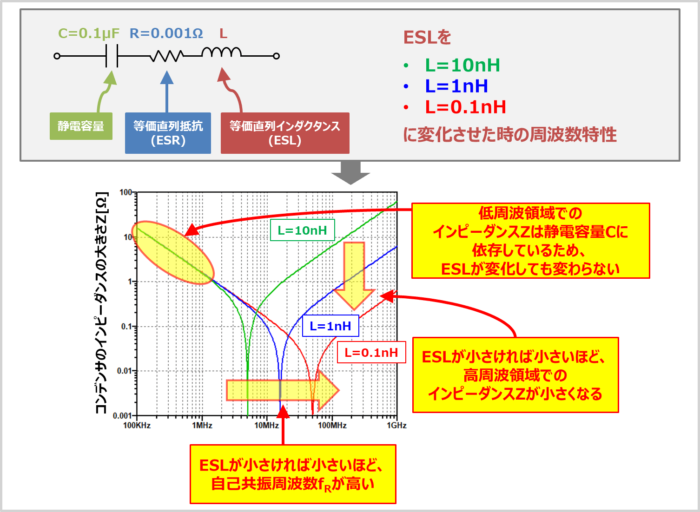

上図にESLのみが変化した時の『周波数特性』を示しています。
一例として、静電容量が『C=0.1μF』、ESRが『R=0.001Ω』のコンデンサにおいて、ESLを『L=10nH、1nH、0.1nH』に変化させています。
ESLのみが変化した時の『周波数特性』を見ると下記のことが分かります。
- 低い周波数でのインピーダンスZは、静電容量Cに依存しているため、ESLが変化しても、変わらない。
- 高い周波数でのインピーダンスZは、ESLが小さければ小さいほど、小さくなる。
- 自己共振周波数fRはESLが小さければ小さいほど、高くなる。
繰り返しになりますが、コンデンサの性能を高い周波数まで有効に働かせるためには、ESLを小さくすることが重要になります。
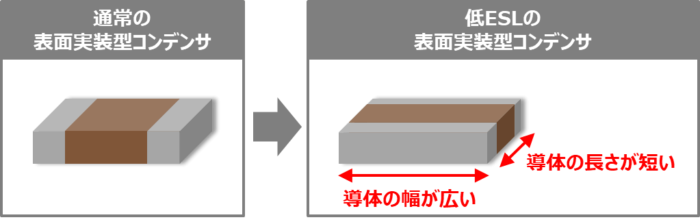
一般的には導体の幅を広くし、導体の長さを短くすればインダクタンスが小さくなるため、下図に示すように縦横を逆にした低ESLの表面実装型コンデンサも商品としてあります。

まとめ
この記事ではコンデンサの『周波数特性』について、以下の内容を説明しました。
- コンデンサの『周波数特性』
- コンデンサの『周波数特性』がV字型になる理由
- 静電容量Cのみが変化した時の『周波数特性』の変化
- ESRのみが変化した時の『周波数特性』の変化
- ESLのみが変化した時の『周波数特性』の変化
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧は以下のボタンから移動することができます。
また、下記に当サイトの人気記事を記載しています。ご参考になれば幸いです。