この記事ではコンデンサCのみ接続した交流回路において
- コンデンサCのみ接続した交流回路の『位相』について
- コンデンサCのみ接続した交流回路の『ベクトル図』の描き方
などを図を用いて分かりやすく説明しています。
コンデンサCのみ接続した交流回路の『位相』
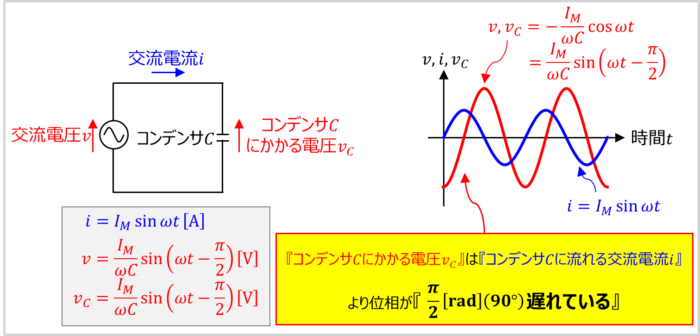
交流電圧\(v\)にコンデンサ\(C\)(静電容量を\(C{\mathrm{[F]}}\)とする)のみ接続した回路を上図に示しています。
コンデンサ\(C\)に交流電圧\(v\)を印加した時、コンデンサ\(C\)に\(i=I_M{\sin}{\omega}t\)の交流電流が流れたとします。
この時、交流電流\(i\)がコンデンサ\(C\)に流れているので、コンデンサ\(C\)にかかる電圧\(v_C\)は次式で表されます。
\begin{eqnarray}
v_C&=&\frac{q}{C}\\
&=&\frac{1}{C}{\displaystyle\int}idt\\
&=&\frac{1}{C}{\displaystyle\int}I_M{\sin}{\omega}tdt\\
&=&\frac{I_M}{C}{\displaystyle\int}{\sin}{\omega}tdt\\
&=&-\frac{I_M}{{\omega}C}{\cos}{\omega}t\\
&=&\frac{I_M}{{\omega}C}{\sin}\left({\omega}t-\frac{{\pi}}{2}\right){\mathrm{[V]}}
\end{eqnarray}
ここで、コンデンサ\(C\)にかかる電圧\(v_C\)は交流電圧\(v\)と等しいので、交流電圧\(v\)は次式で表されます。
\begin{eqnarray}
v=v_C=\frac{I_M}{{\omega}C}{\sin}\left({\omega}t-\frac{{\pi}}{2}\right){\mathrm{[V]}}
\end{eqnarray}
ここで、コンデンサ\(C\)に流れる交流電流\(i\)、交流電圧\(v\)、コンデンサ\(C\)にかかる電圧\(v_C\)をまとめると以下のようになります。
\begin{eqnarray}
i&=&I_M{\sin}{\omega}t{\mathrm{[A]}}\\
v&=&\frac{I_M}{{\omega}C}{\sin}\left({\omega}t-\frac{{\pi}}{2}\right){\mathrm{[V]}}\\
v_C&=&\frac{I_M}{{\omega}C}{\sin}\left({\omega}t-\frac{{\pi}}{2}\right){\mathrm{[V]}}
\end{eqnarray}
すなわち、『コンデンサ\(C\)にかかる電圧\(v_C\)』は『コンデンサ\(C\)に流れる交流電流\(i\)』より位相が\(\displaystyle\frac{{\pi}}{2}{\mathrm{[rad]}}\)(\(90°\))遅れている(言い換えれば、『コンデンサ\(C\)に流れる交流電流\(i\)』は『コンデンサ\(C\)にかかる電圧\(v_C\)』より位相が\(\displaystyle\frac{{\pi}}{2}{\mathrm{[rad]}}\)(\(90°\))進んでいる)ということになります。
位相の『進み』と『遅れ』の見分け方
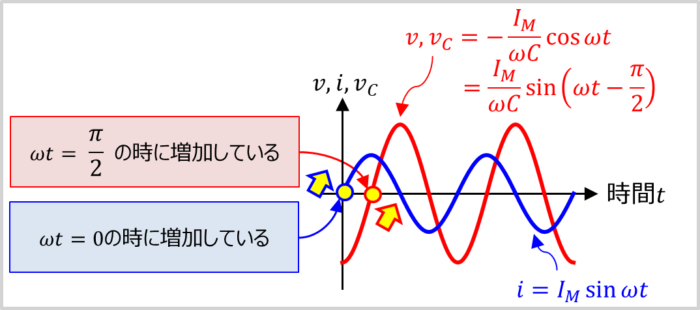
『コンデンサ\(C\)にかかる電圧\(v_C\)』と『コンデンサ\(C\)に流れる交流電流\(i\)』の波形を見れば、位相の『進み』と『遅れ』を簡単に見分けることができます。
『コンデンサ\(C\)にかかる電圧\(v_C\)』は\({\omega}t=\displaystyle\frac{{\pi}}{2}\)の時に増加し始めます。
一方、『コンデンサ\(C\)に流れる交流電流\(i\)』は\({\omega}t=0\)の時に増加し始めます。『コンデンサ\(C\)に流れる交流電流\(i\)』の早く増加していますね。
そのため、『コンデンサ\(C\)に流れる交流電流\(i\)』の方が進んでいることが分かります。
コンデンサCのみ接続した交流回路の『ベクトル図』
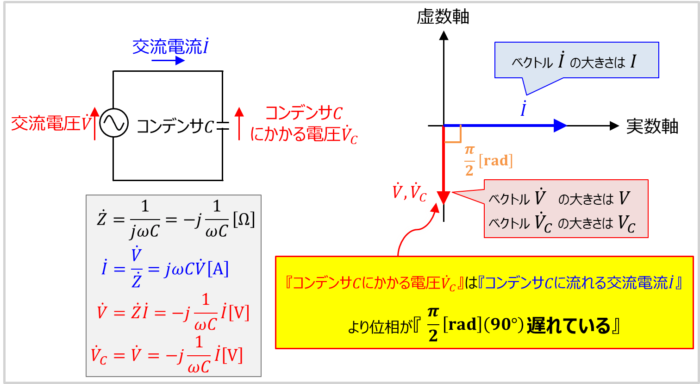
まず、交流電圧\(v\)にインピーダンス\(Z\)を接続した交流回路を考えます。
交流電圧\(v\)のベクトルを\({\dot{V}}\)、インピーダンス\(Z\)のベクトルを\({\dot{Z}}\)、流れる交流電流\(i\)のベクトルを\({\dot{I}}\)とします。この時、交流電圧\({\dot{V}}\)、インピーダンス\({\dot{Z}}\)、交流電流\({\dot{I}}\)は次式の関係があります。
\begin{eqnarray}
{\dot{Z}}&=&\frac{{\dot{V}}}{{\dot{I}}}\\
\\
{\dot{V}}&=&{\dot{Z}}{\dot{I}}\\
\\
{\dot{I}}&=&\frac{{\dot{V}}}{{\dot{Z}}}
\end{eqnarray}
今回は、コンデンサ\(C\)のみ接続した交流回路を考えます。この時、インピーダンス\({\dot{Z}}\)は次式となります。
\begin{eqnarray}
{\dot{Z}}=\frac{1}{j{\omega}C}=-j\frac{1}{{\omega}C}
\end{eqnarray}
したがって、交流電圧\({\dot{V}}\)と交流電流\({\dot{I}}\)は次式となります。
\begin{eqnarray}
{\dot{V}}&=&{\dot{Z}}{\dot{I}}=-j\frac{1}{{\omega}C}{\dot{I}}\\
\\
{\dot{I}}&=&\frac{{\dot{V}}}{{\dot{Z}}}=\frac{{\dot{V}}}{\displaystyle\frac{1}{j{\omega}C}}=j{\omega}C{\dot{V}}
\end{eqnarray}
コンデンサ\(C\)にかかる電圧\(v_C\)のベクトルを\({\dot{V_C}}\)とします。コンデンサ\(C\)にかかる電圧\({\dot{V_C}}\)は交流電圧\({\dot{V}}\)と等しいため、次式で表されます。
\begin{eqnarray}
{\dot{V_C}}={\dot{V}}=-j\frac{1}{{\omega}C}{\dot{I}}
\end{eqnarray}
また、『交流電圧\({\dot{V}}\)の大きさ\(V\)』、『交流電流\({\dot{I}}\)の大きさ\(I\)』、『コンデンサ\(C\)にかかる電圧\({\dot{V_C}}\)の大きさ\(V_C\)』は次式で表されます。
\begin{eqnarray}
V&=&|{\dot{V}}|=\sqrt{\left(\frac{1}{{\omega}C}I\right)^2}=\frac{1}{{\omega}C}I\\
\\
I&=&|{\dot{I}}|=\sqrt{\left({\omega}CV\right)^2}={\omega}CV\\
\\
V_C&=&|{\dot{V_C}}|=\sqrt{\left(\frac{1}{{\omega}C}I\right)^2}=\frac{1}{{\omega}C}I
\end{eqnarray}
ここで、各ベクトルの式と大きさが求まったので、次にベクトル図を描いてみましょう。
『ベクトル図』の描き方
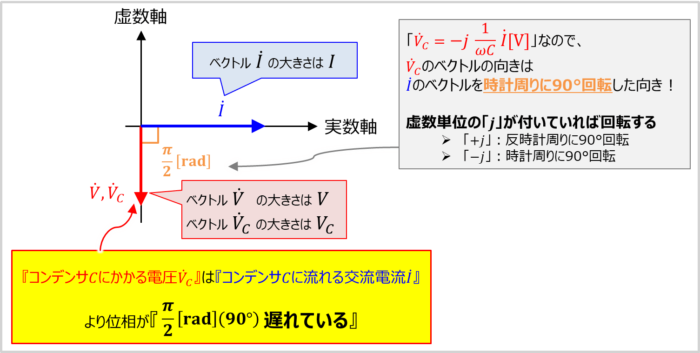
まず、基準とするベクトルを交流電流\({\dot{I}}\)とします。
この時、『コンデンサ\(C\)にかかる電圧\({\dot{V_C}}\)』と『交流電圧\({\dot{V}}\)』のベクトルは以下のように描きます。
- コンデンサ\(C\)にかかる電圧\({\dot{V_C}}\)のベクトル
- 交流電圧\({\dot{V}}\)のベクトル
コンデンサ\(C\)にかかる電圧\({\dot{V_C}}\)は「\({\dot{V_C}}=-j\displaystyle\frac{1}{{\omega}C}{\dot{I}}\)」で表されます。そのため、コンデンサ\(C\)にかかる電圧\({\dot{V_C}}\)のベクトルの向きは交流電流\({\dot{I}}\)のベクトルを時計周りに90°回転した向きになります。コンデンサ\(C\)にかかる電圧\({\dot{V_C}}\)の大きさ(長さ)は交流電流\({\dot{I}}\)を\(\displaystyle\frac{1}{{\omega}C}\)倍したものとなります。
交流電圧\({\dot{V}}\)は「\({\dot{V}}={\dot{V_C}}\)」で表されます。そのため、交流電圧\({\dot{V}}\)はコンデンサ\(C\)にかかる電圧\({\dot{V_C}}\)と向きと大きさが同じになります。
したがって、『コンデンサ\(C\)のみ接続している交流回路』のベクトル図は上図のようになります。
『交流電流\({\dot{I}}\)』に対して、『コンデンサ\(C\)にかかる電圧\({\dot{V_C}}\)』は位相が遅れているということになります。また、『交流電流\({\dot{I}}\)』に対する『コンデンサ\(C\)にかかる電圧\({\dot{V_C}}\)』の位相差は\(-\displaystyle\frac{{\pi}}{2}{\mathrm{[rad]}}\)(\(90°\))となります。
各ベクトルの長さ(大きさ)は、先ほど計算で求めた
\begin{eqnarray}
V&=&|{\dot{V}}|=\sqrt{\left(\frac{1}{{\omega}C}I\right)^2}=\frac{1}{{\omega}C}I\\
\\
I&=&|{\dot{I}}|=\sqrt{\left({\omega}CV\right)^2}={\omega}CV\\
\\
V_C&=&|{\dot{V_C}}|=\sqrt{\left(\frac{1}{{\omega}C}I\right)^2}=\frac{1}{{\omega}C}I
\end{eqnarray}
となります。
ベクトルの向きについて
ベクトルの向きの決め方についてもう少し詳しく説明します。
ベクトルの『向き』について
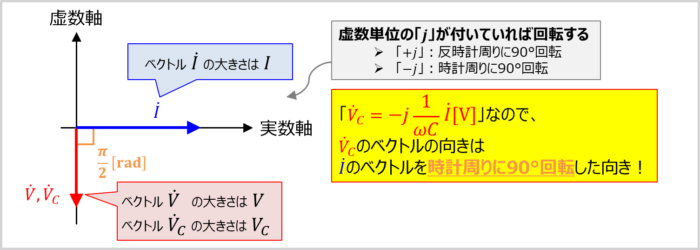
式に虚数単位『\(j\)』が付くとベクトルの向きが90°回転します。
- 『\(+j\)』が付いている時
- 『\(-j\)』が付いている時
ベクトルは反時計周りに90°回転します。
ベクトルは時計周りに90°回転します。
コンデンサ\(C\)にかかる電圧\({\dot{V_C}}\)は「\({\dot{V_C}}=-j\displaystyle\frac{1}{{\omega}C}{\dot{I}}\)」の式で表されます。そのため、ベクトル\({\dot{V_C}}\)の向きはベクトル\({\dot{I}}\)を時計周りに90°回転した向きとなります。
基準ベクトルについて

基準ベクトルについてもう少し詳しく説明します。
基準ベクトルについて
基準ベクトルを\({\dot{A}}\)にした時、ベクトル\({\dot{B}}\)が上記のように回転している場合を考えてみます。
『位相の"進み"と"遅れ"』、『位相差の"正(プラス)"と"負(マイナス)"』は基準ベクトルから『反時計方向に回転しているか』or『時計周りに回転しているか』で下記のように決まります。
- ベクトル\({\dot{B}}\)が反時計方向に回転している場合
- ベクトル\({\dot{B}}\)が時計方向に回転している場合
位相が進んでいるということ。位相差は『正(プラス)』で表します。
位相が遅れているということ。位相差は『負(マイナス)』で表します。
『交流電流\({\dot{I}}\)』を基準ベクトルとして考えると、『コンデンサ\(C\)にかかる電圧\({\dot{V_C}}\)』は時計周りに回転しています。
そのため、『交流電流\({\dot{I}}\)』に対して、『コンデンサ\(C\)にかかる電圧\({\dot{V_C}}\)』は位相が遅れているということになります。また、『交流電流\({\dot{I}}\)』に対する『コンデンサ\(C\)にかかる電圧\({\dot{V_C}}\)』の位相差は\(-\displaystyle\frac{{\pi}}{2}{\mathrm{[rad]}}\)(\(90°\))となります。
一方、『コンデンサ\(C\)にかかる電圧\({\dot{V_C}}\)』を基準ベクトルとして考えると、『交流電流\({\dot{I}}\)』は反時計周りに回転しています。
そのため、『コンデンサ\(C\)にかかる電圧\({\dot{V_C}}\)』に対して、『交流電流\({\dot{I}}\)』は位相が進んでいるということになります。また、『コンデンサ\(C\)にかかる電圧\({\dot{V_C}}\)』に対する『交流電流\({\dot{I}}\)』の位相差は\(+\displaystyle\frac{{\pi}}{2}{\mathrm{[rad]}}\)(\(90°\))となります。
まとめ
この記事ではコンデンサCのみ接続した交流回路について、以下の内容を説明しました。
- コンデンサCのみ接続した交流回路の『位相』について
- コンデンサCのみ接続した交流回路の『ベクトル図』の描き方
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。






