リアクタンスXは「交流回路における電流の流れにくさ」を表します。
一方、サセプタンスBは「交流回路における電流の流れやすさ」を表すものです。この記事ではこのサセプタンスについて
- サセプタンスとは
- サセプタンスの特徴
などを図を用いて分かりやすく説明しています。
サセプタンスとは
最初にサセプタンスの要点を以下にまとめます。
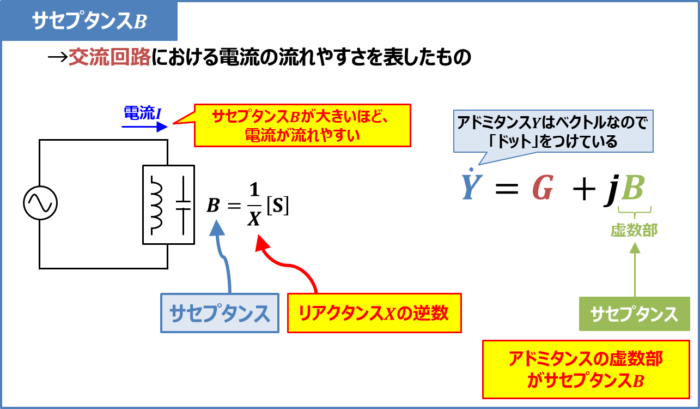
サセプタンスの要点
- サセプタンスはリアクタンスXの逆数であり、記号はB、単位は[S]である
- サセプタンスは大きいほど電流が流れやすくなる
- サセプタンスはアドミタンス(Y=G+jB)の虚数部である
- 『誘導性サセプタンスBL』と『容量性サセプタンスBC』がある
各要点について順番に説明します。
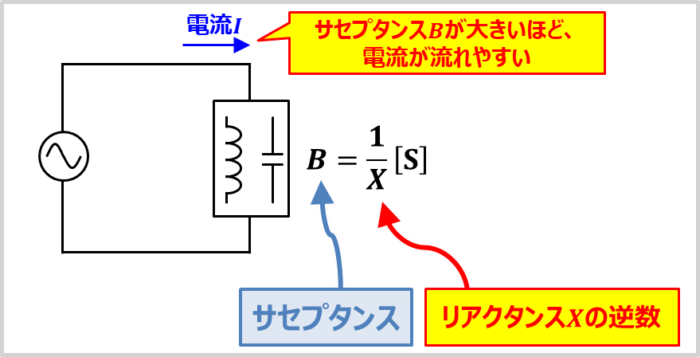
サセプタンスはリアクタンスXの逆数であり、記号はB、単位は[S]である
![サセプタンスはリアクタンスXの逆数であり、記号はB、単位は[S]である](https://detail-infomation.com/wp-content/uploads/2021/03/2c7f81b486e52e604a0145dd712c2037-700x496.png)
サセプタンスは「交流回路における電流の流れやすさ」を表し、リアクタンスXの逆数となります。記号はB、単位は[S](ジーメンス)を用います。式で表すと次式となります。
\begin{eqnarray}
B=\frac{1}{X}{\mathrm{[S]}}\tag{1}
\end{eqnarray}
例えば、10[Ω]のリアクタンスは0.1[S]のサセプタンスと表現することができます。
こで、リアクタンスXは電圧V[V]と電流I[A]の比であるため、次式で表されます。
\begin{eqnarray}
X=\frac{V}{I}{\mathrm{[{\Omega}]}}\tag{2}
\end{eqnarray}
そのため、(2)式を(1)式に代入すると、サセプタンスB[S]を電圧V[V]と電流I[A]で表すことができ、次式となります。
\begin{eqnarray}
B=\frac{1}{X}=\frac{I}{V}{\mathrm{[S]}}\tag{3}
\end{eqnarray}
そのため、サセプタンスB[S]と電圧V[V]が分かれば電流I[A]を求めることができ、サセプタンスB[S]と電流I[A]が分かれば電圧V[V]を求めることができます。
- サセプタンスB[S]と電圧V[V]が分かっている時
- サセプタンスB[S]と電流I[A]が分かっている時
\begin{eqnarray}
I=BV{\mathrm{[A]}}\tag{4}
\end{eqnarray}
\begin{eqnarray}
V=\frac{I}{B}\tag{5}
\end{eqnarray}
サセプタンスは大きいほど、電流が流れやすくなる
リアクタンスXは「交流回路における電流の流れにくさ」を表しています。そのため、リアクタンスXの大きさにより電流Iは以下のように変わります。
- リアクタンスXが大きい
- リアクタンスXが小さい
→電流Iが流れにくい
→電流Iが流れやすい
一方、サセプタンスBはリアクタンスXの逆数なので、「交流回路における電流の流れやすさ」を表しています。そのため、サセプタンスBの大きさにより電流Iは以下のように変わります。
- サセプタンスBが大きい
- サセプタンスBが小さい
→電流Iが流れやすい
→電流Iが流れにくい
また、(5)式ではサセプタンスB[S]と電圧V[V]が分かっている時、流れる電流I[A]は「\(I=BV{\mathrm{[A]}}\)」であることを説明しました。(5)式よりサセプタンスBが大きくなると、電流Iが大きくなることが分かりますね。
サセプタンスはアドミタンスの実数部である

アドミタンスYはコンダクタンスGとサセプタンスBを用いると次式で表されます。
\begin{eqnarray}
{\dot{Y}}=G+jB\tag{6}
\end{eqnarray}
上式より、サセプタンスBはアドミタンスの虚数部であることが分かります。なお、コンダクタンスは『ゼロ』または『正の値』となります。抵抗が接続されていない場合はゼロとなり、抵抗が接続されている場合は抵抗の逆数(正の値)となります。
一方、サセプタンスBは『ゼロ』または『正の値』または『負の値』となります。回路にコンデンサやコイルが接続されていない場合はゼロとなります。また、回路が容量性の場合(コンデンサが接続されている回路)は正の値となり、回路が誘導性の場合(コイルが接続されている回路)は負の値となります。
また、インピーダンスZは次式で表されます。
\begin{eqnarray}
{\dot{Z}}=R+jX\tag{7}
\end{eqnarray}
そのため、(1)式と(8)式と(9)式を用いると次式となります。
\begin{eqnarray}
{\dot{Y}}=\frac{1}{{\dot{Z}}}=G+jB+\frac{1}{R+jX}\tag{8}
\end{eqnarray}
分母を有利化すると、次式に変形することができます。
\begin{eqnarray}
{\dot{Y}}=G+jB&=&\frac{1}{R+jX}\\
&=&\frac{R-jX}{(R+jX)(R-jX)}\\
&=&\frac{R-jX}{R^2+X^2}\\
&=&\frac{R}{R^2+X^2}-j\frac{X}{R^2+X^2}\tag{9}
\end{eqnarray}
すなわち、サセプタンスBは抵抗RとリアクタンスXを用いると次式となります。
\begin{eqnarray}
B=-\frac{X}{R^2+X^2}\tag{10}
\end{eqnarray}
上式において、抵抗Rがゼロの時は下記のようになります。
\begin{eqnarray}
B=-\frac{X}{R^2+X^2}=-\frac{X}{0^2+X^2}=-\frac{1}{X}\tag{11}
\end{eqnarray}
上式において、マイナスが付いているのは、ベクトルを考慮すると「サセプタンスBのベクトルの向き」と「リアクタンスXのベクトルの向き」が逆になるからです。単純に「サセプタンスBの大きさ」と「リアクタンスXの大きさ」で考える場合にはマイナスはつきません。
『誘導性サセプタンスBL』と『容量性サセプタンスBC』がある
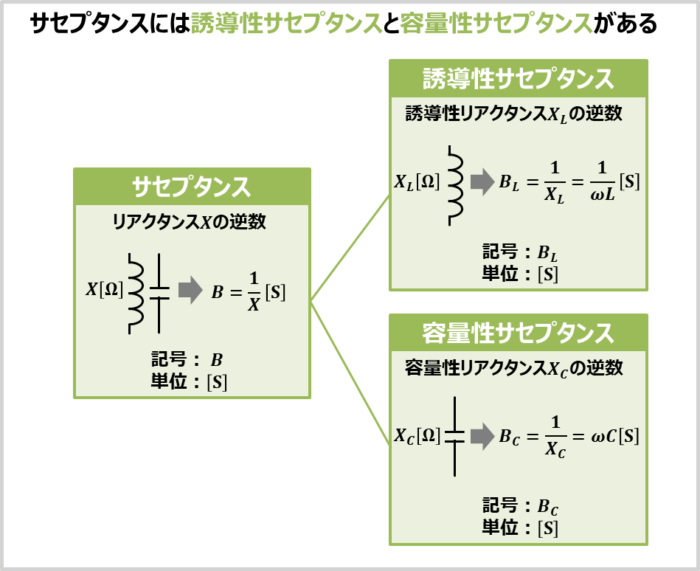
リアクタンスには『コイルのリアクタンス(容量性リアクタンス)XL』と『コンデンサのリアクタンス(容量性リアクタンス)XC』の2種類あり、次式で表されます。
\begin{eqnarray}
X_L&=&{\omega}L{\mathrm{[{\Omega}]}}\\
X_C&=&\frac{1}{{\omega}C}{\mathrm{[{\Omega}]}}
\end{eqnarray}
同様に、サセプタンスにも『コイルのサセプタンス(容量性サセプタンス)BL』と『コンデンサのサセプタンス(容量性サセプタンス)BC』があり、次式の関係があります。
\begin{eqnarray}
B_L&=&\frac{1}{X_L}=\frac{1}{{\omega}L}{\mathrm{[S]}}\\
B_C&=&\frac{1}{X_C}={\omega}C{\mathrm{[S]}}
\end{eqnarray}
まとめ
この記事では『サセプタンス』について、以下の内容を説明しました。
- サセプタンスとは
- サセプタンスの特徴
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。






