この記事ではトランスの結合係数について
- 『結合係数』とは
- 『結合係数』と『相互インダクタンス』の関係
- 『結合係数』と『起電力』の関係
- 『密結合』と『疎結合』について
- 『結合係数』に関する例題
などを図を用いて分かりやすく説明しています。
『結合係数』とは
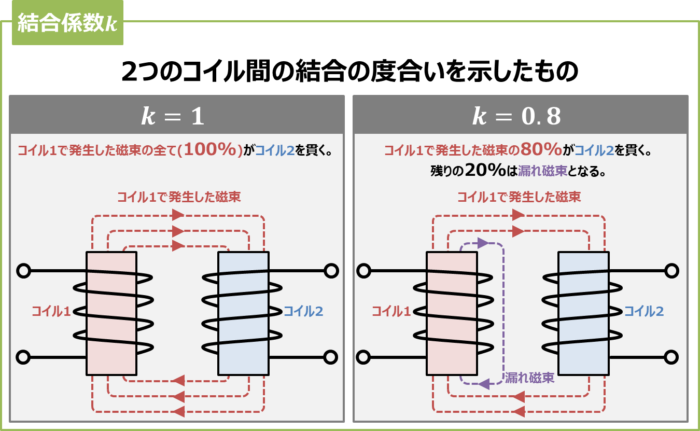
トランス(変圧器)の結合係数は2つのコイル間の結合の度合いを示したものです。記号は『\(k\)』で表します。
上図にコイル1とコイル2の2つのコイルがある図を示しています。
コイル1で発生した磁束の全て(100%)がコイル2を貫く時、結合係数\(k\)は『\(k=1\)』となります。
コイル1で発生した磁束の80%がコイル2を貫く時、結合係数\(k\)は『\(k=0.8\)』となります。コイル1で発生した残り(20%)の磁束は漏れ磁束(漏洩磁束)となります。漏れ磁束はコイル1で発生した磁束のうち、コイル2を貫かなかった磁束です。
このように考えると、結合係数\(k\)が『\(k=0\)』の場合は、コイル1で発生した磁束はコイル2に全く貫かないということになります。すなわち、コイル1で発生した磁束の全てが漏れ磁束になるということです。
そのため、結合係数\(k\)は漏れ磁束の割合を表したものと考えることができます。結合係数\(k\)が1に近いほど、漏れ磁束が少なくなり、\(k=1\)では漏れ磁束が全くないということになります(発生した全ての磁束がコイル2に貫くということ)。
補足
結合係数は英語では「Coupling Coefficient」や「Inductive Coupling Factor」と書きます。
『結合係数』と『相互インダクタンス』の関係
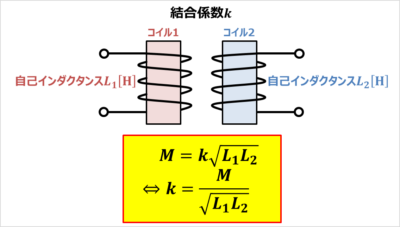
結合係数\(k\)は、コイル1の自己インダクタンスを\(L_1\)、コイル2の自己インダクタンスを\(L_2\)、相互インダクタンスを\(M\)とすると次式で表されます。
\begin{eqnarray}
M&=&k\sqrt{L_1L_2}\\
{\Leftrightarrow}k&=&\frac{M}{\sqrt{L_1L_2}}\tag{1}
\end{eqnarray}
補足
結合係数\(k\)は「漏れ磁束の割合を表したもの(\(k\)が大きいほど、漏れ磁束が少なく、他方のコイルに貫く磁束が多い)」、相互インダクタンス\(M\)は「1つのコイルに電流を流すことで発生する磁束がどれくらい他方のコイルに貫くかを表したもの(\(M\)が大きいほど、他方のコイルに貫く磁束が多い)」であるため、同じような意味となっています。そのため、結合係数\(k\)と相互インダクタンス\(M\)は比例の関係となります。
『結合係数』と『起電力』の関係
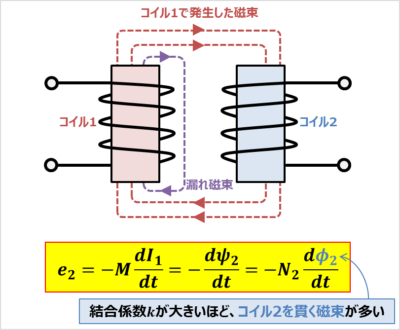
変圧器の二次側(コイル2)の起電力(相互誘導起電力)\(e_2\)は次式で表されます。
相互誘導起電力
\begin{eqnarray}
e_2=-M\frac{dI_1}{dt}=-\frac{d{\psi}_2}{dt}=-N_2\frac{d{\phi}_2}{dt}{\mathrm{[V]}}\tag{2}
\end{eqnarray}
\(e_2\):相互誘導起電力\({\mathrm{[V]}}\)
\(M\):相互インダクタンス\({\mathrm{[H]}}\)(←ヘンリーと読みます)
\(I_1\):コイル1に流れる電流\({\mathrm{[A]}}\)
\(t\):時間\({\mathrm{[s]}}\)
\({\psi}_2\):コイル2の磁束鎖交数\({\mathrm{[wb]}}\)
\({\phi}_2\):コイル2の磁束\({\mathrm{[wb]}}\)
\(N_2\):コイル2の巻数
上式では、コイル2の起電力\(e_2\)はコイル2を貫く磁束\({\phi}_2\)に比例することを示しています。つまり、結合係数\(k\)が大きいほど(漏れ磁束が少なくコイル2に貫く磁束が多いほど)、コイル2の起電力\(e_2\)が大きくなります。
『密結合』と『疎結合』について
結合係数\(k\)が1に近い時、コイル1で発生した磁束\({\phi}_1\)のほとんどがコイル2を貫きます。このような時、2つのコイルの結合は『密』であるといいます(密結合)。このようなトランスを密結合トランス(密結合変圧器)といいます。
結合係数\(k\)が小さい時、コイル1で発生した磁束\({\phi}_1\)の一部しかコイル2を貫くことができません。このような時、2つのコイルの結合は『疎』であるといいます(疎結合)。このようなトランスを疎結合トランス(疎結合変圧器)といいます。
結合係数\(k\)が1に近い時(結合が『密』の時)は(1)式より相互インダクタンス\(M\)が大きく、結合係数\(k\)が小さい時(結合が『疎』の時)は(1)式より相互インダクタンス\(M\)が小さくなります。
『結合係数』に関する例題
問題文
2つのコイルがあり、コイル1の自己インダクタンスが\(L_1=5{\mathrm{[mH]}}\)、コイル2の自己インダクタンスが\(L_2=20{\mathrm{[mH]}}\)、相互インダクタンスが\(M=9.9{\mathrm{[mH]}}\)だった時の結合係数\(k\)はいくらか。
解答
結合係数\(k\)は(1)式を用いると以下の値となります。
\begin{eqnarray}
k&=&\frac{M}{\sqrt{L_1L_2}}\\
&=&\frac{9.9{\mathrm{[mH]}}}{\sqrt{5{\mathrm{[mH]}}×20{\mathrm{[mH]}}}}\\
&=&0.99
\end{eqnarray}
まとめ
この記事ではトランスの結合係数について、以下の内容を説明しました。
当記事のまとめ
- 『結合係数』とは
- 『結合係数』と『相互インダクタンス』の関係
- 『結合係数』と『起電力』の関係
- 『密結合』と『疎結合』について
- 『結合係数』に関する例題
お読み頂きありがとうございました。
当サイトでは電気に関する様々な情報を記載しています。当サイトの全記事一覧には以下のボタンから移動することができます。






