【相互誘導のまとめ】『公式』や『向き』について解説！

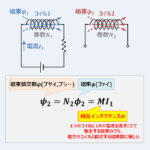
この記事では相互誘導について

相互誘導とは
相互誘導起電力の『公式』
相互誘導起電力の『向き』
相互誘導に関する問題

などを図を用いて分かりやすく説明しています。

相互誘導とは

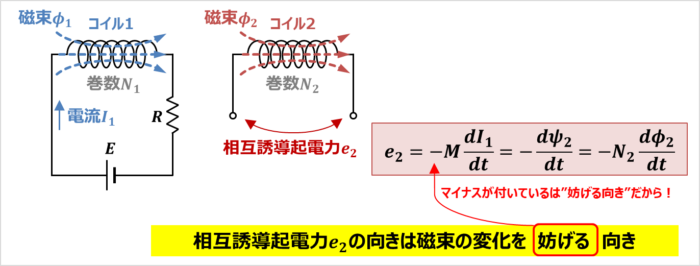
相互誘導は1つのコイルに流れる電流が変化すると、他方のコイルに相互誘導起電力が発生する現象です。相互誘導起電力の向きは磁束の変化を妨げる向きとなります。

上図において、抵抗\(R\)の値や電圧源\(E\)の値を変えることによって、コイル1に流れる電流\(I_1\)を変化させると、コイル2の磁束鎖交数\({\psi}_2\)が変化します。その結果、コイル2に相互誘導起電力\(e_2\)が発生します。

相互誘導起電力\(e_2\)の公式は次式で表されます。

相互誘導起電力の公式

\begin{eqnarray}
e_2=-M\frac{dI_1}{dt}=-\frac{d{\psi}_2}{dt}=-N_2\frac{d{\phi}_2}{dt}{\mathrm{[V]}}\tag{1}
\end{eqnarray}

\(e_2\)：相互誘導起電力\({\mathrm{[V]}}\)
\(M\)：相互インダクタンス\({\mathrm{[H]}}\)(←ヘンリーと読みます)
\(I_1\)：コイル1に流れる電流\({\mathrm{[A]}}\)
\(t\)：時間\({\mathrm{[s]}}\)
\({\psi}_2\)：コイル2の磁束鎖交数\({\mathrm{[wb]}}\)
\({\phi}_2\)：コイル2の磁束\({\mathrm{[wb]}}\)
\(N_2\)：コイル2の巻数

次に相互誘導起電力の向きについて詳しく説明します。

補足

コイル2の磁束鎖交数\({\psi}_2\)、コイル2の巻数\(N_2\)、コイル2の磁束\({\phi}_2\)、相互インダクタンス\(M\)、コイル1に流れる電流\(I_1\)には以下の関係があります。

\begin{eqnarray}
{\psi}_2=N_2{\phi}_2=MI_1
\end{eqnarray}

上式と相互インダクタンス\(M\)について、詳しくは以下の記事で説明していますので、参考にしてください。

: 【相互インダクタンスとは】『単位』や『例題』などを解説！
続きを見る

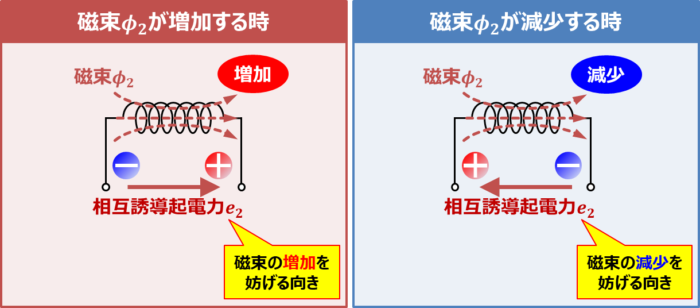
相互誘導起電力の向き

相互誘導起電力\(e_2\)の向きは磁束\({\phi}_2\)の変化を妨げる方向となります。

磁束が増加する時

相互誘導起電力\(e_2\)は磁束の増加を妨げる向きに発生します。上図の場合、相互誘導起電力\(e_2\)は右が「＋」、左が「－」となります。

磁束が減少する時

相互誘導起電力\(e_2\)は磁束の減少を妨げる向きに発生します。上図の場合、相互誘導起電力\(e_2\)は右が「－」、左が「＋」となります。

(1)式にあるマイナスは「磁束\({\phi}\)の変化を"妨げる"」という意味より付けられています。

相互誘導に関する例題

問題文

2つのコイルがあり、相互インダクタンス\(M\)が\(0.5{\mathrm{[H]}}\)とする。この時、コイル1に流れる電流\(I_1\)が\(0.2{\mathrm{[s]}}\)に\(3{\mathrm{[A]}}\)から\(1{\mathrm{[A]}}\)に変化した時、コイル2に発生する起電力\(e_2\)は何ボルトか？

回答

コイル2に発生する起電力\(e_2\)は(1)式を用いると以下の値となります。

\begin{eqnarray}
e_2&=&-M\frac{dI_1}{dt}{\mathrm{[V]}}\\
&=&-0.5×\frac{1-3}{0.2}\\
&=&5{\mathrm{[V]}}
\end{eqnarray}