【ビオ・サバールの法則とは】『直流電流』や『円電流』の磁界の強さの導出など！

この記事ではビオ・サバールの法則について

ビオ・サバールの法則とは
ビオ・サバールの法則の『積分』
直流電流が作る磁界の強さHの導出
円電流が作る磁界の強さHの導出

などを図を用いて分かりやすく説明しています。

ビオ・サバールの法則とは

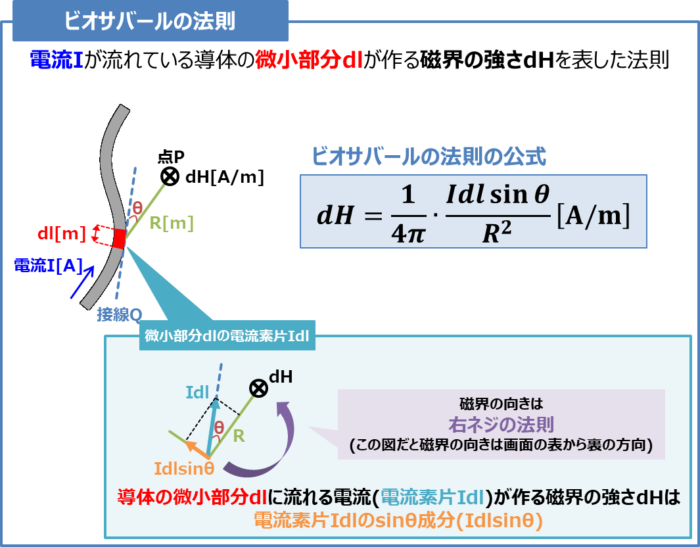
ビオ・サバールの法則とは、電流\(I\)が流れている導体の微小部分\(dl\)が作る磁界の強さ\(dH\)を表した法則です。

上図に示すように、電流\(I{\mathrm{[A]}}\)が流れてる導体において、

導体の微小部分を\(dl{\mathrm{[m]}}\)
導体の微小部分\(dl\)の接線\(Q\)と点\(P\)との角度を\({\theta}\)
導体の微小部分\(dl\)と点\(P\)との距離を\(R{\mathrm{[m]}}\)

とすると、導体の微小部分\(dl\)が点\(P\)に作る磁界の強さ\(dH{\mathrm{[A/m]}}\)は次式となります。

ビオ・サバールの法則の公式

\begin{eqnarray}
dH=\frac{1}{4{\pi}}{\cdot}\frac{Idl{\sin}{\theta}}{R^2}{\mathrm{[A/m]}}\tag{1}
\end{eqnarray}

この上式がビオ・サバールの法則の公式となります。

(1)式より、導体の微小部分\(dl\)が作る磁界の強さ\(dH\)は、電流の大きさ\(I\)、微小部分\(dl\)、\({\sin}{\theta}\)に比例することが分かります。また、クーロンの法則と同様に距離\(R\)の2乗に反比例することが分かります。なお、係数\(\displaystyle\frac{1}{4{\pi}}\)は実験結果から得られた係数となります。

また、導体の微小部分\(dl\)に流れる電流(電流素片\(Idl\))が作る磁界の強さ\(dH\)は『距離\(R\)＆磁界の強さ\(dH\)＆電流素片\(Idl\)』が直角になるようにします。すなわち、『電流素片\(Idl\)の\({\sin}{\theta}\)成分(\(Idl{\sin}{\theta}\))』を考慮する必要があるため、(1)式に\({\sin}{\theta}\)が入っています。

なお、磁界の向きは右ネジの法則で求めます。上図の場合だと、磁界の向きは画面の表から裏の方向となります。

補足

1820年にフランスの物理学者『ジャン＝バティスト・ビオ』と『フェリックス・サバール』によって発見されたため『ビオ・サバールの法則』と呼ばれています。

ビオ・サバールの法則の積分

(1)式で表されるのは、『導体の微小部分\(dl\)が点\(P\)に作る磁界の強さ\(dH\)』であり、『導体全体が点\(P\)に作る磁界の強さ\(H\)』ではありません。

『導体全体が点\(P\)に作る磁界の強さ\(H\)』を求めるためには、『導体の微小部分\(dl\)が点\(P\)に作る磁界の強さ\(dH\)』を足し合わせる必要があります。つまり積分することで求めることができます。

(1)式を積分すると、次式となります。

\begin{eqnarray}
H={\displaystyle\int}dH={\displaystyle\int}\frac{I{\sin}{\theta}}{4{\pi}R^2}dl{\mathrm{[A/m]}}\tag{2}
\end{eqnarray}

上式には積分範囲を記載していません。積分範囲は導体の形(無限長の直流導体や円形コイル)によって変わるためです。

積分範囲を(2)式で考慮することによって、『無限長の直流導体に流れる直流電流が作る磁界の強さ\(H=\displaystyle\frac{I}{2{\pi}r}\)』や『円形コイルに流れる円電流が作る磁界の強さ\(H=\displaystyle\frac{I}{2r}\)』を求めることができるので、次にそれを説明します。

直流電流が作る磁界の強さH

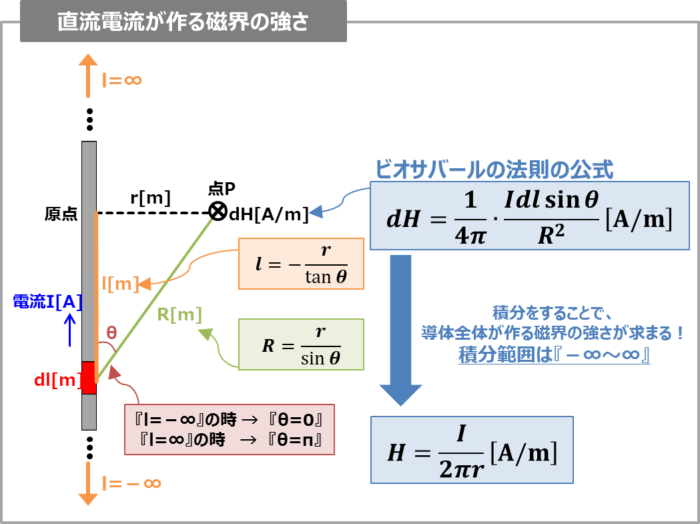
ビオ・サバールの法則を用いて、『無限長の直流導体に流れる直流電流が点\(P\)に作る磁界の強さ\(H\)』を求めるためには、以下の3ステップで求めます。

磁界の強さHを求める3ステップ

導体の微小部分\(dl\)から点\(P\)に対して直線を引く。
導体の微小部分\(dl\)が作る磁界の強さ\(dH\)を求める。
『導体の微小部分\(dl\)が作る磁界の強さ\(dH\)』を積分して『導体全体が作る磁界の強さ\(H\)』を求める。

step
1導体の微小部分\(dl\)から点\(P\)に対して直線を引く

無限長の直流導体において、導体の微小部分\(dl\)から点\(P\)に対して直線を引きます。ここで、

導体の微小部分\(dl\)と点\(P\)との距離を\(R{\mathrm{[m]}}\)
直流導体の原点と点\(P\)との距離を\(r{\mathrm{[m]}}\)
直流導体の原点と導体の微小部分\(dl\)との距離を\(l{\mathrm{[m]}}\)
導体の微小部分\(dl\)と点\(P\)との角度を\({\theta}\)

とします。

step
2導体の微小部分\(dl\)が作る磁界の強さ\(dH\)を求める

この時、導体の微小部分\(dl\)が点\(P\)に作る磁界の強さ\(dH\)はビオ・サバールの公式より次式となります。

\begin{eqnarray}
dH=\frac{1}{4{\pi}}{\cdot}\frac{Idl{\sin}{\theta}}{R^2}{\mathrm{[A/m]}}\tag{3}
\end{eqnarray}

step
3『導体の微小部分\(dl\)が作る磁界の強さ\(dH\)』を積分して『導体全体が作る磁界の強さ\(H\)』を求める

導体の微小部分\(dl\)が作る磁界の強さ\(dH\)を積分することで、導体全体が作る磁界の強さ\(H\)を求めます。

今回、無限長の直流導体の導体全体を考えます。積分範囲は\(-{\infty}～{\infty}\)となるため、(3)式を積分すると次式となります。

\begin{eqnarray}
H={\displaystyle\int}_{-{\infty}}^{{\infty}}dH={\displaystyle\int}_{-{\infty}}^{{\infty}}\frac{I{\sin}{\theta}}{4{\pi}R^2}dl{\mathrm{[A/m]}}\tag{4}
\end{eqnarray}

また、上図より以下の(5)式と(6)式を得ることができます。

\begin{eqnarray}
R{\sin}{\theta}&=&r\\
{\Leftrightarrow}R&=&\frac{r}{{\sin}{\theta}}\tag{5}
\end{eqnarray}

\begin{eqnarray}
l{\tan}{\theta}&=&-r\\
{\Leftrightarrow}l&=&-\frac{r}{{\tan}{\theta}}\tag{6}
\end{eqnarray}

(6)式において、距離\(l\)は原点より下側の領域なのでマイナスをつけています。(6)式を\({\theta}\)で微分すると次式となります。

\begin{eqnarray}
\frac{dl}{d{\theta}}&=&\frac{d}{d{\theta}}\left(-\frac{r}{{\tan}{\theta}}\right)\\
&=&r×\frac{1}{{\tan}^2{\theta}}×\frac{1}{{\cos}^2{\theta}}\\
&=&\frac{r}{{\sin}^2{\theta}}\tag{7}
\end{eqnarray}

また、\(l=-{\infty}\)の時は\({\theta}=0\)、\(l={\infty}\)の時は\({\theta}={\pi}\)となります。

したがって、(5)式と(7)式を(4)式に代入すると、次式となります。

\begin{eqnarray}
H&=&{\displaystyle\int}_{-{\infty}}^{{\infty}}\frac{I{\sin}{\theta}}{4{\pi}R^2}dl\\
&=&{\displaystyle\int}_{0}^{{\pi}}\frac{I}{4{\pi}}×\frac{{\sin}{\theta}}{\left(\displaystyle\frac{r}{{\sin}{\theta}}\right)^2}×\frac{r}{{\sin}^2{\theta}}d{\theta}\\
&=&{\displaystyle\int}_{0}^{{\pi}}\frac{I}{4{\pi}}×\frac{{\sin}^3{\theta}}{r^2}×\frac{r}{{\sin}^2{\theta}}d{\theta}\\
&=&{\displaystyle\int}_{0}^{{\pi}}\frac{I}{4{\pi}r}×{\sin}{\theta}d{\theta}\\
&=&\frac{I}{4{\pi}r}\left[-{\cos}{\theta}\right]_{0}^{{\pi}}\\
&=&\frac{I}{4{\pi}r}\left(-{\cos}{\pi}+{\cos}{0}\right)\\
&=&\frac{I}{4{\pi}r}\left(1+1\right)\\
&=&\frac{I}{2{\pi}r}\tag{8}
\end{eqnarray}

以上より、無限長の直流導体に流れる直流電流が点\(P\)に作る磁界の強さは次式となります。

無限長の直流導体が作る磁界の強さ

\begin{eqnarray}
H=\displaystyle\frac{I}{2{\pi}r}\tag{9}
\end{eqnarray}

円電流が作る磁界の強さH

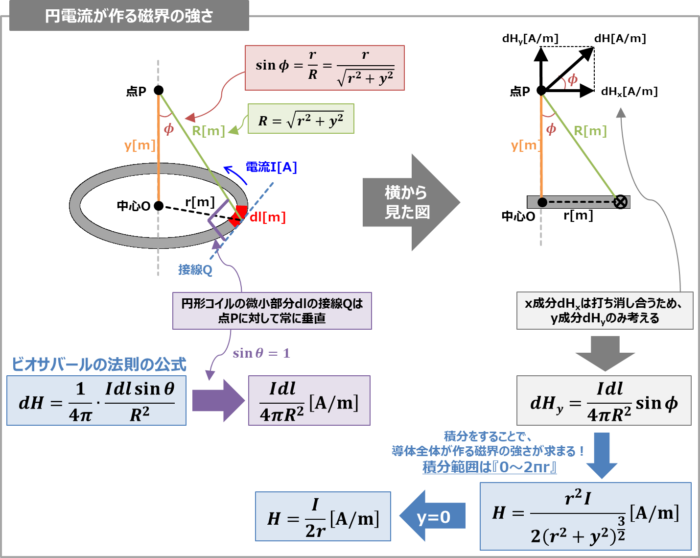
『円形コイルに流れる円電流が点\(P\)に作る磁界の強さ\(H\)』を求める際にも、直流導体と同様に以下の3ステップで求めます。

磁界の強さHを求める3ステップ

導体の微小部分\(dl\)から点\(P\)に対して直線を引く。
導体の微小部分\(dl\)が作る磁界の強さ\(dH\)を求める。
『導体の微小部分\(dl\)が作る磁界の強さ\(dH\)』を積分して『導体全体が作る磁界の強さ\(H\)』を求める。

step
1導体の微小部分\(dl\)から点\(P\)に対して直線を引く

1回巻きの円形コイルにおいて、導体の微小部分\(dl\)から点\(P\)に対して直線を引きます。ここで、

円形コイルの微小部分\(dl\)と点\(P\)との距離を\(R{\mathrm{[m]}}\)
円形コイルの中心\(O\)と点\(P\)との距離を\(y{\mathrm{[m]}}\)
円形コイルの中心\(O\)と導体の微小部分\(dl\)との距離を\(r{\mathrm{[m]}}\)
円形コイルの微小部分\(dl\)と点\(P\)との角度を\({\phi}\)

とします。

step
2導体の微小部分\(dl\)が作る磁界の強さ\(dH\)を求める

この時、導体の微小部分\(dl\)が点\(P\)に作る磁界の強さ\(dH\)はビオ・サバールの公式より次式となります。

\begin{eqnarray}
dH=\frac{1}{4{\pi}}{\cdot}\frac{Idl{\sin}{\theta}}{R^2}{\mathrm{[A/m]}}\tag{10}
\end{eqnarray}

ここで、円形コイルの微小部分\(dl\)の接線\(Q\)は点\(P\)に対して常に垂直(\({\theta}=90°=\displaystyle\frac{{\pi}}{2}{\mathrm{[rad]}}\))となるため、『(\({\sin}{\theta}=1\))』となります。

(10)式の角度\({\theta}\)は上図の角度\({\phi}\)ではなく、微小部分\(dl\)の接線\(Q\)と点\(P\)との角度なので注意してくださいね。

したがって、(10)式は次式となります。

\begin{eqnarray}
dH&=&\frac{1}{4{\pi}}{\cdot}\frac{Idl{\sin}{\theta}}{R^2}\\
&=&\frac{1}{4{\pi}}{\cdot}\frac{Idl×1}{R^2}\\
&=&\frac{Idl}{4{\pi}R^2}\tag{11}
\end{eqnarray}

ここで、上図より\(dH\)のx成分\(dH_{x}\)は微小部分\(dl\)が一周すると全て打ち消し合って『0』となるため、y成分\(dH_{y}\)のみを考えます。\(dH_{y}\)は次式で表されます。

\begin{eqnarray}
dH_{y}&=&dH{\sin}{\phi}\\
&=&\frac{Idl}{4{\pi}R^2}{\sin}{\phi}\tag{12}
\end{eqnarray}

step
3『導体の微小部分\(dl\)が作る磁界の強さ\(dH\)』を積分して『導体全体が作る磁界の強さ\(H\)』を求める

導体の微小部分\(dl\)が作る磁界の強さ\(dH_{y}\)を積分することで、導体全体が作る磁界の強さ\(H\)を求めます。

今回、円形コイルの導体全体を考えます。半径\(r\)の円形コイルの円周は\(2{\pi}r\)より、積分範囲は\(0～2{\pi}r\)となるため、(12)式を積分すると次式となります。

\begin{eqnarray}
H={\displaystyle\int}_{0}^{2{\pi}r}dH_{y}={\displaystyle\int}_{0}^{2{\pi}r}\frac{I}{4{\pi}R^2}{\sin}{\phi}dl{\mathrm{[A/m]}}\tag{13}
\end{eqnarray}

また、上図より以下の(14)式と(15)式を得ることができます。

\begin{eqnarray}
R=\sqrt{r^2+y^2}\tag{14}
\end{eqnarray}

\begin{eqnarray}
{\sin}{\phi}=\frac{r}{R}=\frac{r}{\sqrt{r^2+y^2}}\tag{15}
\end{eqnarray}

したがって、(14)式と(15)式を(13)式に代入すると、次式となります。

\begin{eqnarray}
H&=&{\displaystyle\int}_{0}^{2{\pi}r}\frac{I}{4{\pi}R^2}{\sin}{\phi}dl\\
&=&{\displaystyle\int}_{0}^{2{\pi}r}\frac{I}{4{\pi}\left(\sqrt{r^2+y^2}\right)^2}\frac{r}{\sqrt{r^2+y^2}}dl\\
&=&{\displaystyle\int}_{0}^{2{\pi}r}\frac{rI}{4{\pi}\left(r^2+y^2\right)^\frac{3}{2}}dl\\
&=&\frac{rI}{4{\pi}\left(r^2+y^2\right)^\frac{3}{2}}{\displaystyle\int}_{0}^{2{\pi}r}dl\\
&=&\frac{rI}{4{\pi}\left(r^2+y^2\right)^\frac{3}{2}}\left[l\right]_{0}^{2{\pi}r}\\
&=&\frac{rI}{4{\pi}\left(r^2+y^2\right)^\frac{3}{2}}×2{\pi}r\\
&=&\frac{r^2I}{2\left(r^2+y^2\right)^\frac{3}{2}}\tag{16}
\end{eqnarray}

(16)式は円形コイルの中心軸上において、円形コイルの中心\(O\)から距離\(y\)の位置にある点\(P\)における磁界の強さ\(H\)となります。

ゆえに、円形コイルの中心\(O\)における磁界の強さ\(H\)は(16)式において\(y=0\)を代入すると、

\begin{eqnarray}
H&=&\frac{r^2I}{2\left(r^2+y^2\right)^\frac{3}{2}}\\
&=&\frac{r^2I}{2\left(r^2+0^2\right)^\frac{3}{2}}\\
&=&\frac{r^2I}{2r^3}\\
&=&\frac{I}{2r}\tag{17}
\end{eqnarray}

となります。以上より、円形コイルに流れる円電流が点\(P\)に作る磁界の強さ\(H\)と中心\(O\)に作る磁界の強さ\(H\)は次式となります。

円形コイルが作る磁界の強さ